“Baby, baby, baby ohh … I thought you’d always be mine”, those emo words from Justin Bear Bear Bebe Barber Whoever’s Youtube video rang agonizingly off the study room walls as he stared in vain at his A-Maths notes.
Fresh from a breakup with a girl he’d known since he was 13, he found his eyes constantly flitting from his depressingly boring binomial theorem notes towards a depressingly heartbreaking Neoprint of the two of them taken at Bugis Junction in happier times.
With less than a month to the A-Maths Paper, he’s deep into Last-Minute Buddha Foot Hugging territory. But tried as he might, the scholarly, geeky student just couldn’t focus and that endlessly-looping chorus certainly didn’t help his droopy eyes …
Suddenly the song stopped and a breeze chilled the air in the room, following which he nearly jumped off his chair when he opened his eyes to the sight of a young bespectacled girl seated next to him.
*GASP* Who on EARTH are you?!!!
I’m Miss Loi. Your new maths tutor. Sorry to have startled you.
What??? Tuition now? It’s almost midnight!
With the exams so near and seeing you struggling to get over your breakup, your Mom called my tuition centre for help. Unfortunately we are full but my Sensei decided to send me, an intern tutor, to help you as part of my training. However I can only make it on very late nights so here I am.
Anyway since you seem to be diligently onto your Binomial Theorem notes right now (an oft-misunderstood topic that scared off lots of students due to its complicated and tedious-looking workings at first glance), let’s start on that shall we?
DEMYSTIFYING BINOMIAL THEOREM
The Binomial Expansion
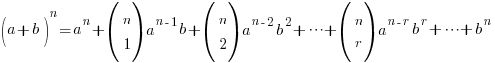
This is given in the formula sheet – don’t waste your brain cells memorising it!
Expression for the r+1th term
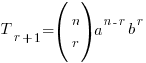
This is NOT given in the formula sheet – but if you can’t remember it you can easily ‘extract’ it from the main binomial expansion expression: 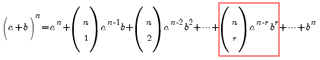
 Don’t simply assume the r+1th term Tr+1 is “the term in xr “!
Don’t simply assume the r+1th term Tr+1 is “the term in xr “!
 The enigmatic “term independent of x“ and the “constant term” both refer to the term that contains x0.
The enigmatic “term independent of x“ and the “constant term” both refer to the term that contains x0.
 Don’t always rush in headlong like a mad dog unleashed to expand the entire expression. Instead, keep the Tr+1 expression in mind when asked to find or compare coefficients of specific terms.
Don’t always rush in headlong like a mad dog unleashed to expand the entire expression. Instead, keep the Tr+1 expression in mind when asked to find or compare coefficients of specific terms.
The nCr Formula
That 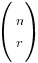 in the binomial expansion is not a matrix. Instead it’s given in the formula sheet as
in the binomial expansion is not a matrix. Instead it’s given in the formula sheet as 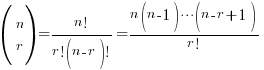
Many students, however, ignore the above KPKB exclamation-laden expression and simply press the button on their calculators – only to meet a tragic end when n is unknown in the question.
So for the sake of the questions where n is unknown, it’s worthwhile to be familiar with the following expressions for up till *nC4:
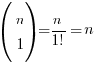
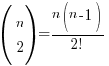
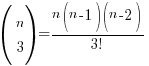
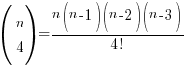
*Most O Level AMaths binomial questions only require you to deal with up to the first 4 terms, but don’t take my word for it 🙂 In any case, you should be able to ‘see’ the pattern for the expressions and use the button on your calculator to find that factorial (!) in the denominator if you need to obtain nCr expressions beyond the first 4 terms.
OK this, plus a firm grasp of your Rules of Indices, is ALL you need to know for Binomial Theorem!
Huh? That’s all? Like this I can also be a tutor myself! I wonder why Mom decided to engage you … hey where have you gone???
The student looked up to find that she had suddenly vanished.
I’m not done yet.
Turning around, he nearly fell off from his chair again at the sight of her seated behind him.
The Four Basic Binomial Theorem Questions
‘O’ Level AMaths binomial questions generally fall into four types, though a combination of them may be asked within the same question:
[+] A. Expand & Multiply
This is the classic binomial question where you expand an expression up to the first couple of terms, and then use your partial expansion to obtain the expansion of more a complicated expression. You may or may not be told how many terms to expand to, but you almost always should NEVER attempt to expand the entire expansion, especially if the powers are high.
Find, in ascending powers of x, the first 3 terms in the expansion of
(a) (1 + 4x)6 (b) (1 − 2x)14
Hence find the expansion of (1 + 4x)6(1 − 2x)14 up to the terms in x2.
ANS: Using the Binomial Expansion formula given in your formula sheet,
(a) (1 + 4x)6
= 16 + 6C1(15)(4x) + 6C2(14)(4x)2 + …
= 1 + 6(1)(4x) + 15(1)(16x2) + …
= 1 + 24x + 240x2 + …
(b) (1 − 2x)14
= 114 + 14C1(113)(−2x) + 14C2(112)(−2x)2 + …
= 1 − 14(1)(2x) + 91(1)(4x2) + …
= 1 − 28x + 364x2 + …
To obtain the first 3 terms of (1 + 4x)6(1 − 2x)14, we multiply and expand (1 + 24x + 240x2 + …)(1 − 28x + 364x2 + …) but we must know when to stop multiplying!
Know when enough is enough!
Since we’re only interested in terms up to x2, we ignore all combos that result in powers of x > 2 and kick them into oblivion for trying to waste your precious exam time!
(1 + 24x + 240x2 + …)(1 − 28x + 364x2 + …)
= 1(1 − 28x + 364x2) + 24x(1 − 28x + 364x2) + 240x2(1 − 28x + 364x2)
= 1 − 28x + 364x2 + 24x − 672x2 + 240x2
= 1 − 4x − 68x2
 This is when your intimate knowledge of indices is called upon, especially with trickier expressions containing more than one x and inverse powers of x e.g.
This is when your intimate knowledge of indices is called upon, especially with trickier expressions containing more than one x and inverse powers of x e.g. 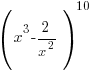
 Sometimes you’re NOT told how many terms to expand, but simply told to e.g. “expand up to and including the terms in x3” or “given that (1 + 4x)6(1 − 2x)14 = a + bx + cx2 + …, find a, b and c.” In such cases, you’re expected to know from the start how many terms to expand to, but for the sake of your future NEVER, EVER kill yourself by trying to expand the entire expression, especially when the powers are high e.g. (1 − 2x)14
Sometimes you’re NOT told how many terms to expand, but simply told to e.g. “expand up to and including the terms in x3” or “given that (1 + 4x)6(1 − 2x)14 = a + bx + cx2 + …, find a, b and c.” In such cases, you’re expected to know from the start how many terms to expand to, but for the sake of your future NEVER, EVER kill yourself by trying to expand the entire expression, especially when the powers are high e.g. (1 − 2x)14
Tekan Revision Exercise
Find the term independent of x in the expansion 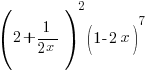 .
.
[Answer: −3]
[+] B. Expand & Substitute
Instead of ‘Expand & Multiply’ describe above, this time you expand and substitute a suitable value/expression into your expansion in order to expand a more complicated expression, estimate a value, and achieve world peace.
ANS: Using the Binomial Expansion formula given in your formula sheet,
(1 − p)5
= 15 + 5C1(14)(−p) + 5C2(13)(−p)2 + 5C3(12)(−p)3 + 5C4(12)(−p)4 + (−p)5
= 1 − 5p + 10p2 − 10p3 + 5p4 − p5
Do the Substitution!
To make (1 − x + x2)5 be like (1 − p)5, we equate 1 − p with 1 − x + x2:
⇒ 1 − p = 1 − x + x2
⇒ p = x − x2 → our substitute expression!
So sub p = x − x2 into the expansion:
= 1 − 5(x − x2) + 10(x − x2)2 − 10(x − x2)3 + 5(x − x2)4 − (x − x2)5
→ we’re only interested in terms up to x3, so we ignore all combos that result in powers of x > 3 to save time
= 1 − 5x + 5x2 + 10(x2 − 2x3 + x4) − 10(x3 + …)
→ Yay! Don’t have to expand that cubic expression as there’s only one x3 term in (x2 − 2x3 + x4)(x − x2)
= 1 − 5x + 5x2 + 10x2 − 20x3 − 10x3 + …
= 1 − 5x + 15x2 − 30x3 + …
Substitute again!
To estimate (1.11)5 using x, we equate 1.11 with 1 − x + x2
⇒ 1.11 = 1 − x + x2
⇒ x2 − x − 0.11 = 0
Solving the quadratic equation, x = −0.1 or 1.1
In order to use (1 − x + x2)5 = 1 − 5x + 15x2 − 30x3 + … to estimate (1.11)5, it’s better to use x = −0.1 since its higher powers are comparatively smaller enough to be ignored i.e. −0.14 = −0.0001 vs 1.14 = 1.4641
∴ (1.11)5 ≈ 1 − 5(−0.1) + 15(−0.1)2 − 30(−0.1)3 ≈ 1.68
[+] C. Finding Specific Terms
This is the kind of question where you’re asked to find “the term in x10“, “the term independent of x“, “the constant term”, “the coefficient of x4” etc. from a straightforward (a + b)n expression (vs the multiplied (a + b)n(c + d)m in preceding examples).
This is when the r+1th Term formula must instantly possess your mind, so that you curb your expansionary instincts and control yourself – don’t rush in blindly like a mad dog unleashed to expand the entire expression to the detriment of your precious exam time!
In the expansion of 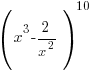 , find
, find
(a) the term in x10
(b) the coefficient of 
(c) the constant term
ANS: This is a straightforward (a + b)n expression ⇒ NO expansion is necessary (Control yourself! You don’t want to die young expanding this to the power of 10!)
Derive the General Tr+1 ‘Formula’ for the Expression
The key is to first derive a general Tr+1 ‘formula’ for this from the r+1th Term formula and simplify it using, once again, some indices magic:
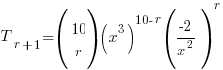
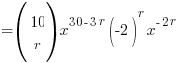
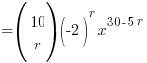
⇒ power of x = 30 − 5r
And now, armed with this almighty expression for the power of x, you find yourself in ‘God Mode’ where, by a simple substitution of r with a suitable value, nothing, absolute nothing, can stand between you and the solutions to parts (a), (b) and (c) 😈 Muahahaha!
(a) For x10, 30 − 5r = 10 ⇒ r = 4
∴ term in x10 = 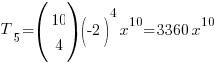 (Muahahaha!)
(Muahahaha!)
→ x10 is included in the final answer since we are finding the term
(b) For x−5, 30 − 5r = −5 ⇒ r = 7
∴ coefficient of x−5 = 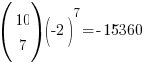 (Muahahahaha!!!)
(Muahahahaha!!!)
→ x−5 is NOT included in the final answer since we are finding the coefficient
(c) For the constant term x0 (which is also the oft-used “term independent of x“), 30 − 5r = 0 ⇒ r = 6
∴ constant term = 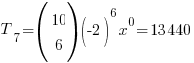 (MUAHAHAHAHA!!! :twisted:)
(MUAHAHAHAHA!!! :twisted:)
→ we don’t include x0 in the final answer since it is a constant
Feels great to be powerful isn’t it? But please don’t write “Muahahaha” on your actual answer script 😛
Tekan Revision Exercise
(i) In the binomial expansion of 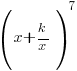 , where k is a positive constant, the coefficients of x3 and x are the same. Find the value of k.
, where k is a positive constant, the coefficients of x3 and x are the same. Find the value of k.
(ii) Using the value of k found in part (i), find the coefficient of x7 in the expansion of 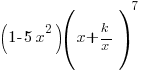
[Answer: k = 3/5, Coefficient of x7 = −20]
[+] D. When n is Unknown …
Whenever n is unknown, it’s almost certain that you’ll have to expand the nCr Formula into the 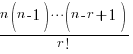 form within an expansion or Tr+1 formula (that calculator button will suddenly become useless for those who like to keep pressing it), to obtain the value of n and some other variables via the comparison of the coefficients of suitable terms.
form within an expansion or Tr+1 formula (that calculator button will suddenly become useless for those who like to keep pressing it), to obtain the value of n and some other variables via the comparison of the coefficients of suitable terms.
ANS: (1 + ax)n = 1n + nC11n−1(ax) + nC21n−2(ax)2 + …
→ since there’s only one x term with non-negative power in the expression, we only need to expand to the first 3 terms
= 1 + nax + 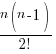 a2x2 + …
a2x2 + …
→ instead of trying to derive from the definition of nCr given in the formula sheet, being familiar with the nC1 to nC4 expressions will be handy here.
Compare Coefficients
Comparing our own expansion with the given expansion,
na = −12 —– (1) → compare coefficients of x
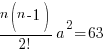 —– (2) → compare coefficients of x2
—– (2) → compare coefficients of x2
Sub a = −12/n into (2):
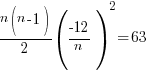
9n = 72
∴ n = 8
Sub n = 72 into (1):
∴ a = −12/8 = 3/2
Tekan Revision Exercise
In the expansion of (2 + 3x)n, the coefficients of x3 and x4 are in the ratio 8 : 15. Find the value of n.
[Answer: n = 8]
[+] Summary Exercise
To round things off, now that you have understood the 4 kinds of binomial questions I’ve just taught you, you should be able to solve (with one of your eyes closed) this question from the 2009 GCE ‘O’ Level AMaths Paper 2 that had somehow resulted in massive outpouring of grief among those who took the paper that year.
(i) Write down the first three terms in the expansion, in ascending powers of x, of 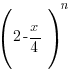 , where n is a positive integer greater than 2.
, where n is a positive integer greater than 2.
The first two terms in the expansion, in ascending powers of x, of 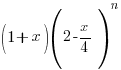 are a + bx2, where a and b are constants.
are a + bx2, where a and b are constants.
(ii) Find the value of n.
(iii) Hence find the value of a and b.
[Answer: n = 8, a = 256, b = −144]
Now make sure you hand in your completed homework the next time I see you or you’ll be surprised at the nasty stuff I can do to you! I’ll be watching you ….
The Justin Bleah Bleah song started playing again, waking him from his slumber.
Realizing that he must have been talking in his sleep again, he wiped away the disgusting saliva that had stained his sleeve, before proceeding to attempt a couple of those depressingly-humorless questions in his binomial notes.
And then he suddenly realized that those questions actually fall into four main types …




 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















5 Comments
曜
日
Help! I have some questions about rounding off of answers. When doing Math and A Math paper, unless otherwise stated, is it true that candidates should
- leave final answers (other than in degrees) to 3 significant figures ONLY if the answer is not exact. E.g. 74.5 / 4, do we leave our final answer as 18.625 since it is exact?
- use at least 4 significant figures to do working, and if the working includes figures that have been rounded off to 4sf, the final answer should be corrected to 3sf even if it appears as a fraction which is exact?
- answers in money should be rounded off to the nearest cent and not 3 significant figures e.g. $245.67 and not $246 (3sf)?
曜
日
@Aaron: I think i can help a little
1. It's exact, no 3 sf
2. Miss Loi answer this
3. Yes, But miss loi may have a better answer
P.s: Miss Loi, another nice post by you, but you left out "evil smile" the maclaurin series for rational or negative indicies, but nvm....
曜
日
@TJK: maclaurin series?! in O levels now? gosh!
曜
日
@mathslover: Think he study his H2 Maths until 走火入魔 already ...
曜
日
@Aaron: *tap tap your shoulder*
My Sensei has answered your questions over at the relevant blog post.
Also, your other questions on the 2009 E-Maths Paper 1 suggested solutions have been moved here.
*vanishes*