*tap tap tap* “moi ish sad … feel sho moddy … ”
*tap tap tap* “GPGT! here’s a chio bu peekture to cheer u up”
*tap tap tap* “wah! ![]()
![]()
![]() SIC sauce leh ~~~
SIC sauce leh ~~~ ![]() ”
”
*tap tap tap* “this zehzeh i got from exampap …”
WAKE UP!!!
Once again, he nearly fell off his chair.
Your O Levels are barely a week away and you still have time to chat in that Hardwarezone forum?!
Sorry lah Miss Loi. I’m still trying to get over my breakup okay? My grades used to be good when I studied together with my Girl Girl. But now I’m just feeling lonely 🙁
Suddenly he felt his neck being shaken violently by a pair of invisible hands.
For the sake of your future, you must not be distracted and keep your FOCUS for the next few weeks! After that, you can surf all the
变态Hardwarezone forums to your heart’s content!
Upon seeing his soulless lovesick eyes, however, she knew that her words (and violent shaking) had no effect on him and decided that some drastic action needed to be taken. So she took a glance at his Neoprint, removed her glasses and chanted something unintelligible to herself …
Boy Boy …
When he turned around and saw the girl standing before him, he was stunned.
Girl Girl! It’s you!
Boy Boy Darling, now that I’m here to 陪 you to study, are you able to focus now? Good. Since you’re feeling … umm … MODDY let’s start talking about Modulus Functions today shall we? It’s getting late.
Modulus Functions
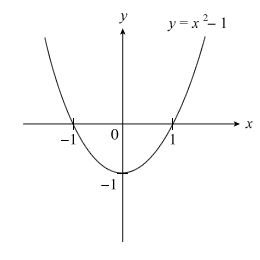
Re-introduced into the New AMaths 4038 Syllabus since 2008 following the removal of a once-mighty chapter called Functions *distant thunder could be heard at the mention of this word*, modulus functions these days mostly involve freeing variables trapped within |modulus signs|, and the sketching of V-, W-shaped modulus graphs.
[+] The Basics
|a| ≥ 0
⇒ |a| = a if a ≥ 0 → useful in simplifications to immediately remove mod brackets when a is confirm chop stamp positivee.g. |√6 − √3| + |√3 − √6| = √6 − √3 + |√6 − √3| = 2√6 − 2√3|a| = |−a| (NOTE: |a| ≠ −|a|!)
→ this gives us |a−b| = |b−a| which is useful for bringing out common factors|ab| = |a||b|
→ always remember to keep the mod sign when bringing out constants & variables i.e. DON’T do this:|−2(x−1)| = −2|(x−1)| → WRONG!
|−2(x−1)| = |−2||(x−1)| = 2|(x−1)| ✔|x(x−1)| = x|(x−1)| → WRONG!
|x(x−1)| = |x||(x−1)| ✔

→ same warning applies as per Property 2 above.|an| = |a|n
→ this gives us |a|2 = a2 which is useful for removing the mod sign via ‘squaring both sides’. However the mod sign stays for odd powers i.e. |a|3 ≠ a3!
[+] Removing Modulus Signs and Solving Modulus Equations
Rearrange/simplify (e.g. via bringing out common factors) so that at most one pair of mod signs appears on either side i.e.
|f(x)| = g(x), f(x) = |g(x)|, |f(x)| = |g(x)|Slowly … but surely … slide those modulus signs off to form two equations i.e.
|f(x)| = |g(x)| ⇒ f(x) = g(x) or f(x) = −g(x)Solve the two equations.
*Check and reject any value of x that is not valid for the original equation.
→ many missed out this step which is especially IMPORTANT for equations with x on both sides, where one side must be positive but not the other.
Sample Questions
[+] ANSWER
2|x − 2| + |7||2 − x| = 9 → bring out the common factor x−2 via |ab|=|a||b|
2|x − 2| + 7|x − 2| = 9
→ |x − 2|=|2 − x| (now you know why they’re common factors 😉 )
9|x − 2| = 9
|x − 2| = 1
x − 2 = 1 or x − 2 = −1 → Modulus sign removed!
∴ x = 3 or 1
[+] ANSWER
|(x + √6)(x − √6)| = −5x → |a||b| = |ab|
|x2 − 6| = −5x
x2 − 6 = −5x or x2 − 6 = 5x → Modulus sign removed!
x2 + 5x − 6 = 0 or x2 − 5x − 6 = 0
(x − 6)(x + 1) = 0 or (x + 6)(x − 1) = 0
x = 6, −1, −6, 1
 Before you merrily hop away, STOP & CHECK!
Before you merrily hop away, STOP & CHECK!
The LHS of the equation is always positive but the RHS can be negative if x is 1 or 6. Hence we reject 1 and 6.
∴ x = −1, −6
[+] Removing Modulus Signs in Inequalities
In general, modulus inequalities in ‘O’ Level AMaths are usually solved via the graphical approach. But just in case some question-setter wakes up on the wrong side of the bed, these two expressions are almost always used to remove the modulus signs should you ever encounter the need to solve a modulus inequality via a non-graphical approach:
- |f(x)| < k ⇔ −k < f(x) < k [explanation diagram]
- |f(x)| > k ⇔ f(x) > k or f(x) < −k [explanation diagram]
Check out this past question to see how this is applied. Else skip to the graphical approach that is more likely to be used in your exam (but don’t blame me if it turns out otherwise!).
Understand so far?
My Girl Girl … when can we go Bugis Junction to take Neoprints again?
Not till your O Levels are over Dear … now let’s move on to Modulus Graphs, shall we?
Graphs of Modulus Functions
[+] Sketch → Reflect → Flip → Shift!
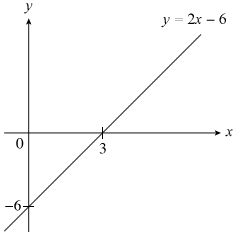
AMaths modulus graphs are usually of the form
To sketch them, we do NOT waste time drawing up a table of values but instead perform the following steps (which must be done in order):
- SKETCH: sketch only the part of the expression within the modulus signs i.e. f(x)
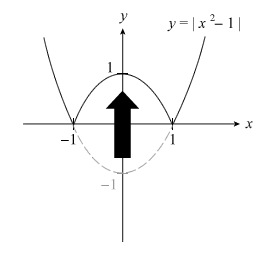
- REFLECT: reflect in the x-axis only the portion below it − you should get a V-shape graph (if f(x) is linear) or a W-shape graph (if f(x) is quadratic)
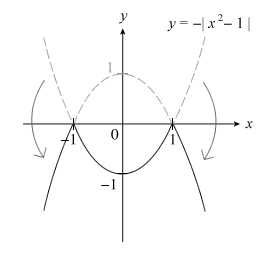
- FLIP: flip the entire graph in the x-axis to get a Λ-shape or M-shape graph. This step is only required if there’s a negative sign (−) before the modulus sign!
- SHIFT: shift the entire graph upwards(+C units) or downwards (−C units) along the y-axis. This step is only required if C is not zero!
Sample Sketches
Pay attention to how the equation changes in the diagrams.
[+] ANSWER
SKETCH!
Sketch the graph for the part of the expression that’s within the modulus sign.
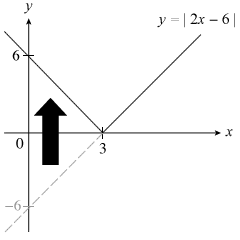
REFLECT!
Using the x-axis like a mirror, reflect in the x-axis the portion of the line that’s below it. Notice the sign of the y-intercept changing from −6 to 6.
FLIP!There’s no negative sign before the modulus sign, so we skip the flipping step.
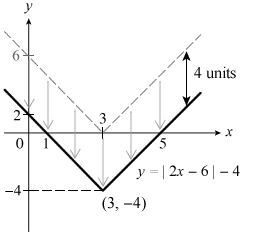
SHIFT!
There’s a constant (−4) outside the modulus sign, so we shift the graph downwards by 4 units along the y-axis. Notice all the y-coordinates have changed by −4 units.
N.B. Remember to calculate (by setting x/y = 0 etc., as learnt in your EMaths) and label all your intercept and turning points and axes in your final sketch as a good graph sketcher ought to do!
[+] ANSWER
SKETCH!
Sketch the graph for the part of the expression that’s within the modulus sign.
REFLECT!
Mirror, mirror on the x-axis, reflect all the negativity that’s below it!
The Olympic-Style FLIP!
There’s a negative sign before the modulus sign, so we must flip the entire graph in the x-axis. This is somewhat similar to the Reflect step before this, only that the entire graph is reflected here (vs only the negative portion). Notice that the only point(s) that remain(s) unchanged after the Olympic-style flip is/are the x-intercept(s).
SHIFT!
There’s a constant (+2) outside the modulus sign, so we shift the graph upwards by 2 units along the y-axis.
Once again, remember to label all your intercept and turning points and axes in your final sketch as a 乖乖 graph sketcher ought to do!
[+] Finding Coordinates in Modulus Graphs
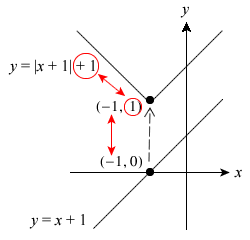
From the modulus graph sketches above, it should be fairly obvious in the final graphs that, for the x-intercepts, the x-coordinates remain unchanged while the y-coordinates are equal to the constant outside the modulus sign.
This enables us to determine quickly the coordinates of the sharp turning point(s) of modulus graphs.
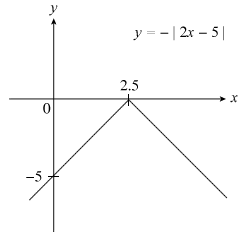
[+] ANSWER
From the equation, you should be able straightaway obtain the coordinates C(−6, −2) in a record-breaking 1.0 × 10−100 seconds!
Too fast for you? OK …
x-intercept of 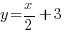 is (−6, 0) → obtained via
is (−6, 0) → obtained via 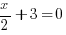
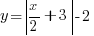 basically shifts
basically shifts 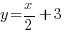 downwards by 2 units
downwards by 2 units
⇒ its y-coordinate ↓ 2 units, its x-coordinate is unchanged → it has become the ‘sharp’ turning point of the modulus graph
⇒ C(−6, −2)
Coordinates for the intercepts A and B are found via simply setting x=0 and y=0 respectively, as learnt in your EMaths Coordinate Geometry.
Sub x = 0: y = |0/2 + 3| − 2 = 1 ⇒ A(0, 1)
Sub y = 0: |x/2 + 3| − 2 = 0
|x/2 + 3| = 2
x/2 + 3 = 2 or x/2 + 3 = −2 → you still remember how to remove the modulus sign right?
x = −2 or −10
From the graph, B(−10, 0)
[+] Modulus Graph Ranges & Inequalities
As mentioned previously, you’re more likely to solve a modulus inequality using a graphical approach, which is arguably a ‘safer’ method since you can really ‘see’ and convince yourself of the validity of the ranges in question.
This usually entails
- Sketching a modulus graph for a range of values of x – you’ll still be performing the same Sketch → Reflect → Flip → Shift acrobatic sequence but now there’s an extra step of including only the part of the graph bounded by the given range of x – which means you’ll also have to calculate and include in the final sketch the corresponding range of values of y.
- STARING at the graph(s) with your eyes open till you attain enlightenment as to the range you’re looking for.
Sample Question
Sketch the graph of y = −|2x − 5| for −1 < x ≤ 4. State the range of values of x for which y > −3.
[+] ANSWER
We’ll fast-forward and condense the Sketch → Reflect → Flip → Shift sequence and present the sketch for y = −|2x − 5| in a single diagram. TADA!
Now we calculate the values of y when x = −1 and 4.
Sub x = −1: y = −|2(−1) − 5| = −7
Sub x = 4: y = −|2(4) − 5| = −3
So we take only the portion of the graph that falls within −1 < x < 4 as our final sketch, with the corresponding values of y as indicated.
NOTE:
- Though many TYS solutions don’t do this, it’s always a good practice to insert the relevant circles at the extreme ends of the graph to indicate whether it’s ● (inclusive) or ○ (not inclusive).
- Some may prefer to calculate the boundaries and sketch y = 2x − 5 for the range first, before proceeding to Reflect → Flip → Shift within the boundaries to obtain the final sketch. There’s no right or wrong sequence to this as long as you don’t end up plotting a table of values!
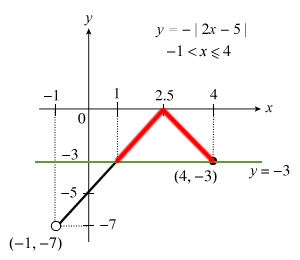
Potential Goondu Moment: If you’re asked to state the corresponding range of y in this case, it’s −7 < y ≤ 0 NOT −7 < y ≤ −3!!! That’s why you must always STARE at the graph with your eyes open!
To find the range of x where y > −3, instead of trying to solve the inequality −|2x − 5| > −3 (and wondering at the end if your > < signs are pointing in the right directions), we simply draw the horizontal line y = −3 across the sketched graph and then proceed to STARE at it with your eyes big big:
If you’ve stared at it long enough, it’ll be as clear as the diamond on my Sensei‘s earring that you’re looking at the portion of y = −|2x − 5| that’s above y = −3 (shown in red).
Now all that’s left to do is to find the value(s) of x where the lines meet i.e.
−|2x − 5| = −3
|2x − 5| = 3
2x − 5 = 3 or 2x − 5 = −3
x = 4, 1.
∴ From the sketch, when y > −3, 1 < x < 4
Wow this turned out to be quite a long session today. I certainly hope my 口水 has not been in vain.
My Girl Girl … when can we go Bugis Junction to take Neoprints again?
*facepalm* Is that all you can say?!
Now do this question as part of your homework tonight!
Summary Question
- Solve |(x − 1)(x − 4)| = 2
- Sketch the graph of y = |(x − 1)(x − 4)|. Find the range of values of x for which y = |(x − 1)(x − 4)| < 2.
[Answer: i. 0.439, 2, 3, 4.56 ii. 0.439 < x < 2 or 3 < x < 4.56]
Oh by the way, where’s your completed homework for last week’s Binomial Theorem?
…
Where is it huh? Huh? HUH???!!! You want to feel moddy again?
… errr … my Girl Girl … when can we go Bugis Junction to take Neoprints again?
An unearthly scream was heard in the neighbourhood that night …


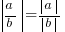
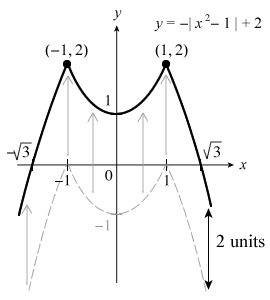
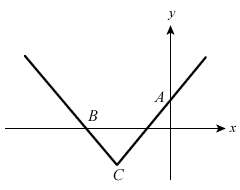
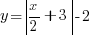 . Find the coordinates of points A, B and C.
. Find the coordinates of points A, B and C.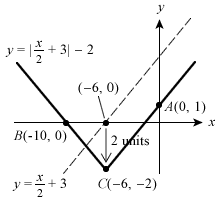
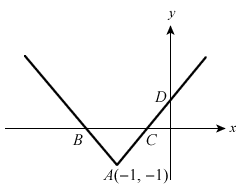
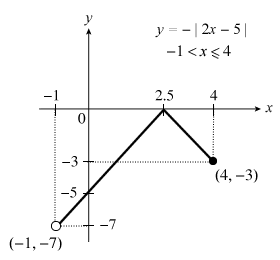
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 




















