A long time ago (okay not that long) in an old A-Maths Syllabus far, far away, there was an evil topic called Relative Velocity – where a mere mention of its name would strike fear into the hearts of students, caused teachers to quit, and made babies cry at night.
So one can imagine the national euphoria that reached epic proportions when the said topic was removed from the New Syllabus …
… only to be replaced by another fiendish nightmare called Plane Geometry (or Geometric Proofs to some) that’s causing widespread pandemonium for students across the nation, making teachers stutter in class, and … umm … the babies haven’t stopped crying.
While it’s easy to say that everything you need to know is summarized in the following (along with this Similarity & Congruency chart):
The reality, however, is quite often that mortals like you and me will probably stare and stare at the Plane Geometry question till we end up like this:
But we suppose that a ‘killer’ topic like this is meant to separate the haves from the have-nots in that cumulative frquency curve, for only those on the brink of their Mathematical Nirvana will get to experience that life-changing moment of sudden realization, when you reach your Mathematical high, and your knees begin to tremble as you feel the power of the Midpoint/Intercept Theorem flowing through your body as you look up to see a glowing image of Miss Loi amongst the clouds in the sky.

If you desire to join Stephen Chow, Cristiano Ronaldo and whoever’s that Miss Universe in these emotive Plane Geometry moments, you must develop the 阴阳眼 of Plane Geometry, for the signs within those complex geometrical diagrams will only reveal themselves magically to those who possess it, and only then will you be able to ‘see’ eerie things that others don’t.
Contrary to the myth that one can only be born with it (as suspected in most foreign cyborgs cases), the 阴阳眼 (lit. Yin Yang Eye) can actually be acquired through long hours of old-fashioned practice.
To that end, Miss Loi has toiled through the week to string together the following series of Plane Geometry questions that she sincerely hope can help improve your ‘eyesight’ in time for your O-Level A-Maths papers this week.
THE PLANE GEOMETRY EYESIGHT TEST
 PLEASE DO NOT CLICK ON THE ANSWERS BEFORE YOU’VE ATTEMPTED THE QUESTION! You will NEVER be able to develop the 阴阳眼 by merely reading through the answers!
PLEASE DO NOT CLICK ON THE ANSWERS BEFORE YOU’VE ATTEMPTED THE QUESTION! You will NEVER be able to develop the 阴阳眼 by merely reading through the answers!
For a start, don’t always insist on jumping in with the latest theorems. Sometimes all you need are just the basic geometrical properties you’ve learnt in your primary school and Sec One Maths (see part 1 of this question).
Also when you see an obvious lack of circles in the diagram, be prepared to seek out and use the Intercept Theorem or the Midpoint Theorem at some point.
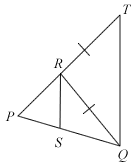
In the given figure, RT = RQ. If SR bisects ∠PRQ,
- Prove that ∠PRS = ∠RTQ.
- Show that
 .
.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
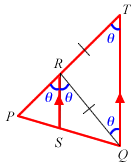
Let ∠RTQ = ∠RQT = θ (∠s of isosceles Δ)
⇒ ∠PRQ = 2θ (ext. ∠ = sum of interior opposite ∠s of Δ)Since SQ bisects ∠PRQ,
⇒ ∠PRS = ∠QRS = θ
⇒ ∠PRS = ∠RTQAnd since ∠PRS = ∠RTQ
⇒ RS // TQ (corresponding ∠s)Using Intercept Theorem,
 (∵ RQ = RT)
(∵ RQ = RT)
Instead of folding your arms and stare and stare at the diagram till you turn into stone, things can magically appear when you finally decide to lift up that 100kg pencil of yours to draw a couple of lines to join up all points in the diagram, for fortune tends to favour those who can lift and use their pencils.
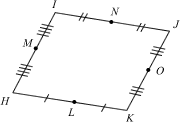
Given a quadrilateral HIJK, let L, M, N and O denote the respective midpoints. Show that LMNO is a parallelogram.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
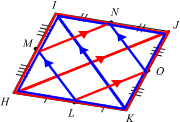
MN // MN // LO (Midpoint Theorem)
NO // IK // ML (Midpoint Theorem)
⇒ LMNO is a parallelogram (∵ MN // LO & NO // ML
Ditto for this next question. You’ll be amazed how much 天机 (Heaven’s Will) is revealed by a single (correct) stroke of fate. Moreover, you’ll also discover that most Plane Geometry solutions are pretty short (typically 1-2 steps) since each part usually carries only 3-5 marks.
It’s the 阴阳眼 that you need!
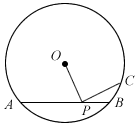
The diagram shows a circle with centre O and a chord AB. P is on AB and C is on the circle such that ∠OPC = 90°.
Prove PC2 = PA∙PB
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
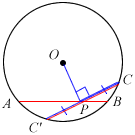
Extending the line PC to C’,
C’P = PC (Perpendicular bisector of chord)
⇒ C’P∙PC = PA∙PB (Intersecting Chords Theorem)
⇒ PC2 = PA∙PB (∵ C’P = PC)
Once again, join up the points dear – join up those points!
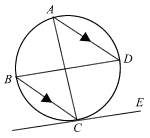
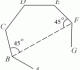
ABCD is a cyclic quadrilateral. CE is a tangent to the circle at C. Given that AD // BC, prove that
- ∠BCA = ∠DCE
- ∠ABC = ∠BCD
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
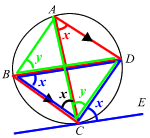
∠DCE = ∠DBC (Alternate Segment Theorem)
∠DBC = ∠DAC (∠s in same segment)
∠DAC = ∠BCA (alternate ∠s)
⇒ ∠BCA = ∠DCELet ∠DCE = x
⇒ ∠DBC = x (Alternate Segment Theorem)
⇒ ∠ACB = x (alternate ∠s)
Let ∠ABD = y
⇒ ∠ACD = y (∠s in same segment)∴ ∠ABC = x + y = ∠BCD
Have your eyes warmed up sufficiently by now? Can you now see ‘them’ now in the more complicated diagram below? Yes, they’re everywhere, crying out to you.
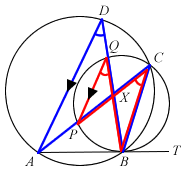
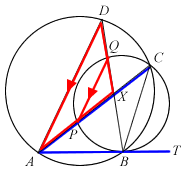
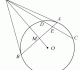
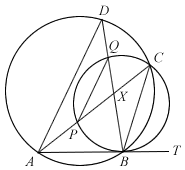 ABT is a tangent to circle PBCQ. The circles ABCD and PBCQ intersect at B and C. APC and BQD are straight lines intersecting at X.
ABT is a tangent to circle PBCQ. The circles ABCD and PBCQ intersect at B and C. APC and BQD are straight lines intersecting at X.
- Prove that PQ is parallel to AD.
- Show that
 .
.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!

∠ACB = ∠ADB (∠s in same segment)
∠PQB = ∠ACB (∠s in same segment)
⇒ ∠ADB = ∠PQB (corresponding ∠s)∴ PQ // AD

Since PQ // AD,
 (Intercept Theorem)
(Intercept Theorem)

Also,
AC∙PA = AB2 (Tangent Secant Theorem)

∴
And now one of the so-called ‘killer’ question to wrap things up.
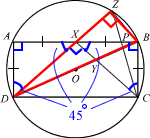
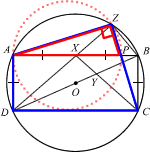
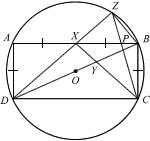 ABCD is a rectangle whose vertices lie on the circumference of a circle, centre O. X is the midpoint of AB, and AD = AX. Y lies on BD and XYC is a straight line. Z lies on the circumference of the circle and DXZ is a straight line. AC and BD intersect at O. The line CZ meets AB at P.
ABCD is a rectangle whose vertices lie on the circumference of a circle, centre O. X is the midpoint of AB, and AD = AX. Y lies on BD and XYC is a straight line. Z lies on the circumference of the circle and DXZ is a straight line. AC and BD intersect at O. The line CZ meets AB at P.
- Prove that ΔDXY is similar to ΔDZB.
- Explain why a circle that passes through A, P and Z can be drawn.
[+]  ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!
ANSWER – you shall suffer a terrible fate if you click and peek at the answer before you’ve tried the question!

ΔDXY and ΔDZB share ∠ZDB.
∠DZB = 90° (∠ in semi-circle)
∠AXD = ∠BXC = (180°-90°)/2 = 45° (interior ∠s of isosceles Δ)
⇒ ∠DXC = 180°-45°-45° = 90° (adjacent ∠s)
⇒ ∠DXC = DZB
⇒ ∠DYX = DBZ (sum of interior ∠s of Δ)
⇒ ΔDXY similar to ΔDZB (AAA)
∠AZP = 180°-∠ADC (=90°) = 90° (Opposite ∠s of cyclic quadrilateral)
⇒ a circle that passes through A, P and Z (∵∠AZP is ∠ in semi-circle)
Most of the theorems have been covered till this point. And if you’ve successfully proven all the questions ON YOUR OWN, your knees will tremble as you receive that almighty gift of the 阴阳眼 Of Plane Geometry, knowing that no Plane Geometry question can stop you from now on.
If you don’t, you’ll just have to try the above questions all over again till you do 😉
Most importantly to all O-Level A-Maths students, may you find your 阴阳眼 in your A-Maths Papers this week!
P.S. Little Miss Loi wishes all Science students good luck for your O-Levels too!



 .
.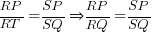 (∵ RQ = RT)
(∵ RQ = RT)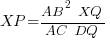 .
.
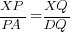
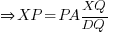
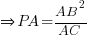
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















23 Comments
曜
日
HAR it got taken out!? (is part of the "long time ago", cough. it REALLY wasn't that long ago. really. REALLY!)
Young people nowadays are so lucky!
曜
日
Yes, yes Wendy hence that "(okay not that long)" coz we'd all agree that it REALLY wasn't that long ago - in fact it was just last year 😉
But think most Physics students would still prefer Relative Velocity leh.
曜
日
i is just the thing i am looking for.
my weakest chapters in amath is plane geometry and sketching of graphs. they are killing me.
曜
日
I just went through the whole thing... and I couldn't get a single one T_T. This type of plane geometry is x10 harder than the p.g. in the United States =( *sob*
曜
日
Don't worry Lisa ! Just 1hr + away from Amaths Paper II and I can't do any of the questions either =(. But don't worry, I pray that God will grant us mercy and grace, to let us have that sudden 阴阳眼 for the particular question later on.
=D
曜
日
ash + rispwaker: Were you gifted the 阴阳眼 that allowed you to 'see' that eerie Mid-Point Theorem triangle on Friday?
Lisa: You sure these are 10x harder than those in the US? Miss Loi has just received some sample Geometric Proof questions from Hong Kong and oh my ... o.O Think AMaths students there require 阴阳 Lasik surgery 😛
曜
日
*cough... I did. I was was tossing and turning, swirling and revolving the entire paper, in hope of that 阴阳眼 would come.
And before I knew... an invigilator came stomping towards me. I could sense impeding doom, and just as he stood before me. I looked at her, then looked back at my paper, and OH GOSH! I SAW THE MID-POINT THEOREM ! It must be because of her solemn yet suggestive stare at me, that the 阴阳眼 popped out.
Well, but knowing is one thing, explaining is another. I just merely wrote some nonsense, then suddenly, pop in a midpoint theorem ( I did not know how to prove that mid-point theorem was valid), in hope that the old and foggy cambridge markers would just look at the GOLDEN *Mid-Point Theorem* and give me that valuable 5 marks.
曜
日
hmm i thought it was similar triangles to solve that mid point problem.
one triangle has radius as a side. one triangle has diameter as a side. prove ratio 2:1.
曜
日
I saw the mid-point theorem after 10 minutes of and staring at the paper... The paper was at 2.30pm and i slept at 1am the night before so my 阴阳眼 cannot activate immediately =.=
My steps are proving 2 lines parallel using corresponding angle and then since O is midpoint, E is midpoint...is it correct?
曜
日
Well, no one knows for sure, until MISS Loi makes her holy appearance and show us the light out of this question.
曜
日
p.s. i forgot to type the word so my sentence sounds weird.... The 1st statement should read: I saw the mid-point theorem after 10 minutes of MEDITATION and staring at the paper
曜
日
Yeah Miss Loi, the plane geometry learned here includes theorems my teachers never covered before (e.g. alternate segment theorem, midpoint theorem, intercept theorem) in the US. We don't call it plane geometry in the US though... the topic is called proofs. We need to write out two columns, Statements & Reasons... then prove what is asked, similar to this topic. It also involves circles and triangles... One thing easier about S'pore proofs is that it's much easier writing it out after you've figured out how to solve the problem. In the US, you write LOADS for your proof. If you have a long problem, it might take half a page... writing out... things such as...
ABC is a right angle - Perpendicular lines intersect to form right angles
DEF is a right angle - Perpendicular lines intersect to form right angles
ABC is equal to DEF - All right angles are equal
Lameee =.=
and rispwaker, I'm not taking the O-levels this year haha... I just moved from the US a few weeks ago here and I'm hoping to enroll in a good JC in Singapore =_=. So in order to know what I should already know going into JCs, I should completely master O-level math (which I am failing). ;(
曜
日
I think it would be quite challenging to find a JC here, since you just came from United States. ( Education here is tough. No joke. )
But anyways, all the best to you. <3
曜
日
Alright everyone, by popular request here's Miss Loi's solution to the inaugural Plane Geometry aka Geometric Proof question of the GCE O' Level 2008 AMaths Paper II.
*DENG DENG DENG DENG ...*
First, the question:
The diagram shows a circle, centre O, with diameter AB. The point C lies on the circle. The tangent to the circle at A meets BC extended at D. The tangent to the circle at C meets the line AD at E.
[+] ANSWER - The same rule applies here: you shall suffer a terrible fate if you click and peek at the answer before you've tried the question!
ANSWER - The same rule applies here: you shall suffer a terrible fate if you click and peek at the answer before you've tried the question!
Answer to Part i.
OE (Common side)
OA = OC (Radius of circle)
AE = CE (Tangents from external point)
EAO = ECO = 90° (Radius ⊥ tangent)
Just pick the relevant ones from the pasar malam of points above to prove that ΔAEO ≡ ΔCEO via SSS or SAS case!
Now for the answer to Part ii:
*Summons the mighty 阴阳眼*
Since O is the mid-point of AB, so if E is the mid-point of AD, then like what Anoneemers said all we need is to prove OE // BD for the Mid-point Theorem to hold.
Let ∠ABC be θ.
*Summons the mighty 阴阳眼 again *
Looking at the arc AC, ∠AOC = 2θ (∠ at centre = 2 x ∠ at circumference)
⇒ ∠AOE = θ (ΔAEO ≡ ΔCEO)
⇒ OE // BD (∵ ∠AOE = ∠ABC → corresponding ∠s)
So by the Mid-point Theorem, E is the mid-point of AD. YAY!
But do note that the above is by no means the only way to prove that E is the mid-point of AD.
Like what mido said, you can also prove that ΔAEO and ΔADB are similar, and thereby using the ratio:
to deduce that E is the mid-point of AD. But Miss Loi's fingers are a little too tired now to type out the proof for the similarity part 😛
Anyone with more otherworldly 阴阳眼 experiences to share from Friday???
P.S. Miss Loi hopes that rispwaker's 阴阳眼 on Friday was really zooming in on the AMaths paper and not at some suggestive spot on the invigilator.
曜
日
There's another 阴阳眼 question on Friday which is the 9(i) proving L=4sinθ-2cosθ (p.s. this is not plane geometry) and alot of people dunno how to prove because they see right angles on 2 sides and then they thought is kite =.= then i was thinking if its a kite then L=2cm which is impossible...
So i drew many many lines n eventually got the answer
曜
日
whoa whoa whoa, when was that photo taken
曜
日
Anoneemers: Yes there should be more than one way to prove L in that kite-ish diagram in 9(i). Did your 阴阳眼 saw the same stuffs as Miss Loi's?
Crazyhamster: Believe it or not, it was found via searching for "stressed student" in Google Images!
Google may have picked you as the iconic symbol of all stressed Singaporean students!
曜
日
Err okay maybe this is a little late to say this, but there seems to be a small typo with question 1...
The question reads: "In the given figure, RT = RQ. If SQ bisects ∠PRQ" when it kinda looks more like SR bisecting ∠PRQ...
Part 2:
The question asks to show that (RT/RQ) = (SP/SQ)... but isn't RT = RQ?
I dunno, maybe I'm just hallucinating the mistakes or something :S
曜
日
Thanks Calvin for pointing out the typos.
Yes in Qn 1, SR should be the angle bisector and the said ratio in the question has been amended to .
.
And it's not you but Miss Loi who was actually hallucinating when she was typing this whole chunk of swollen-fingers-inducing article many weeks ago 😛
Do ring the bell loud loud again should you spot any more typos.
曜
日
Okay. So my vision's still working perfectly 😛
曜
日
Erm for the 4th question,is it possible to conclude that
angle ABC=angle BCD=90 degree by using the right angle in semi circle theorem?
曜
日
JH: For your conclusion to be true, AC & BD have to be diameters of the circle in order for ABC & BCD to be semi-circles, but this is not given in the question.
Also note that though CE is tangent to the circle at C, it's not stated in the question that AC is ⊥ to CE, so we can't assume AC to be a diameter using the radius ⊥ tangent property either.
However, do share with Miss Loi any alternative method should your own 阴阳眼 happens to reveal something different 😉
曜
日
Miss Loi I like the way u express your proof with diagrams. Thanks for the geometry formula sheet I have never seen one. With the diagrams of both I will be able to teach geometry even to the youths who can't read.