
(click to enlarge)
With less than ten days (at the time of writing) to go, the skies darkened as the wind picked up, tossing helpless NTUC Fairprice plastic bags up and down like a stock market, as old symptoms (and a couple of new ones) began to surface once more.
While the world deals with the small matter of the possible disintegration of its global financial system, students at Miss Loi’s Temple have far more important things to worry about, like that big A-Maths Integration chapter.
Eh Miss Loi, how come these two Integration questions I never see before in my TYS one?
*Narrowly dodging the big Shing Lee A-Maths textbook that came hurling straight at his face He sat upright and was all ears …
Ooi! Dreaming of your crush again?!
You should know by now that two elements from the New A-Maths Syllabus have impishly made their way into the Integration chapter!
GEN-Y INTEGRATON
A. Integration of 1/(ax + b)
Starting this year, we have a new entry to the Integration scene:
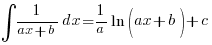 —– (A1)
—– (A1)Having signed a formidable pact with Partial Fractions, the integrals will generally appear in the form of
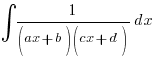 or
or 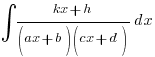
i.e. only linear factors/repeated linear factors in the denominator – very unlikely you’re see quadratic factors like (x2+b2) unless it’s a Hence question with a big clue in the first part.
So whenever you encounter something like the above, regardless of whether you’ve been explicitly told by the question to do so, you MUST perform your Partial Fractions 三大招式 (Three Devastating Moves) to express it in partial fractions first before proceeding to integrate using (A1) above.
SAMPLE QUESTION
Express
 in partial fractions. Hence evaluate
in partial fractions. Hence evaluate  .
.Ans:
Expressing in partial fractions (reference here for the steps if you’re unsure):
- Check: degree of (8x+13) = 1 < degree of (1+2x)(2+x)2 = 3
⇒ PROPER (YAY!) 
→ 1 x linear factor (1+2x) and
→ 1 x repeated linear factor (2+x)2Multiply both sides by (1+2x)(2+x)2,
8x+13 = A(2+x)2 + B(1+2x)(2+x) + C(1+2x)Sub x = -2, -½ … blah blah blah … we get

 For all rogue Cover-Up Rule users, note that you can only use it to find the corresponding partial fractions for the terms with linear factors and the higher order of repeated linear factors
For all rogue Cover-Up Rule users, note that you can only use it to find the corresponding partial fractions for the terms with linear factors and the higher order of repeated linear factorse.g. For this question you can use the Cover-Up rule to find
 and
and  but NOT
but NOT  .
.
So,


And now you can unleash the expression (in (A1) above) upon these integrals!
 At this point, many students will ‘ln ln ln’ till they’ve forgotten how to integrate the 3rd term i.e. the 1/(2+x)2.
At this point, many students will ‘ln ln ln’ till they’ve forgotten how to integrate the 3rd term i.e. the 1/(2+x)2.Remember this?

![{} = 4 delim{[}{{1/2}ln(1+2x)}{]}^2_1 - 2delim{[}{ln(2+x)}{]}^2_1 - delim{[}{1/{2+x}}{]}^2_1 {} = 4 delim{[}{{1/2}ln(1+2x)}{]}^2_1 - 2delim{[}{ln(2+x)}{]}^2_1 - delim{[}{1/{2+x}}{]}^2_1](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20210%20140%22%3E%3C/svg%3E)
![{} = 2 delim{[}{ln 5 - ln 3}{]} - 2 delim{[}{ln 4 - ln 3}{]} - delim{[}{1/4 - 1/3}{]} {} = 2 delim{[}{ln 5 - ln 3}{]} - 2 delim{[}{ln 4 - ln 3}{]} - delim{[}{1/4 - 1/3}{]}](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20210%20140%22%3E%3C/svg%3E)

- Check: degree of (8x+13) = 1 < degree of (1+2x)(2+x)2 = 3
- Now can you try evaluating
 ? 😉
? 😉
B. Integrating Trigonometric Functions Using FURTHER TRIGONOMETRIC IDENTITIES
Basic Rules of Integrating Trigonometric Functions
Firstly, you should all know these by now:

 – note the minus sign!
– note the minus sign!
-

![{}= int{}{}{delim{[}{sec^2 (ax + b) - 1}{]}} dx {}= int{}{}{delim{[}{sec^2 (ax + b) - 1}{]}} dx](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20210%20140%22%3E%3C/svg%3E) (∵ sec2x = 1 + tan2x)
(∵ sec2x = 1 + tan2x)

Starting this year, however, strange forms of trigonometric functions may be pleading for your integrating wizardry in the O-Levels e.g. 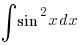 ,
, 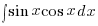 ,
, 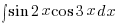 etc.
etc.
These are brought to you courtesy of the new Trigonometric Identities of the new syllabus, namely the Double Angle Formulae, Addition Formulae and the Factor Formulae.
While these formulae will be provided in your exam, you’re likely to find yourself frequently using the following derived Double Angle expressions to solve these new wave integration problems:
 —– (B1)
—– (B1) —– (B2)
—– (B2) —–(B3)
—–(B3)
Armed with these, we can now join the Gen-Y Integration Movement!
SAMPLE QUESTIONS
 – Using (B3) above
– Using (B3) above
![{} = {1/2} int{}{}{delim{[}{1 - cos 2x}{]}} dx {} = {1/2} int{}{}{delim{[}{1 - cos 2x}{]}} dx](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20210%20140%22%3E%3C/svg%3E)

 – Using (B1) above
– Using (B1) above




![{} = {1/2}int{}{}{delim{[}{sin 5x - sin x}{]}} dx {} = {1/2}int{}{}{delim{[}{sin 5x - sin x}{]}} dx](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20210%20140%22%3E%3C/svg%3E)
(Using Factor Formula sin A sin B = 2 cos ½(A+B) sin ½(A–B) )

Now can you evaluate these? 😉
P.S. Check out this online integrator for quick answers to your integration problems.
 *LAST BUT NOT LEAST Miss Loi is too gentle and demure to even harm an ant, much less hurl big Shing Lee textbooks at daydreaming students.
*LAST BUT NOT LEAST Miss Loi is too gentle and demure to even harm an ant, much less hurl big Shing Lee textbooks at daydreaming students.


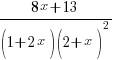 in partial fractions. Hence evaluate
in partial fractions. Hence evaluate 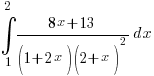 .
.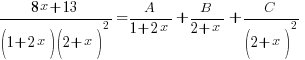
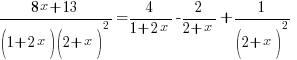
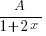 and
and 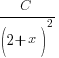 but NOT
but NOT 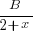 .
.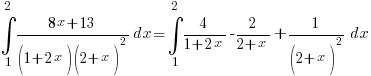
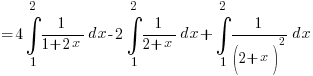
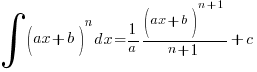
![{} = 4 delim{[}{{1/2}ln(1+2x)}{]}^2_1 - 2delim{[}{ln(2+x)}{]}^2_1 - delim{[}{1/{2+x}}{]}^2_1 {} = 4 delim{[}{{1/2}ln(1+2x)}{]}^2_1 - 2delim{[}{ln(2+x)}{]}^2_1 - delim{[}{1/{2+x}}{]}^2_1](https://www.exampaper.com.sg/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_963_dad8653c57748392fcd112bdae07b2ac.png)
![{} = 2 delim{[}{ln 5 - ln 3}{]} - 2 delim{[}{ln 4 - ln 3}{]} - delim{[}{1/4 - 1/3}{]} {} = 2 delim{[}{ln 5 - ln 3}{]} - 2 delim{[}{ln 4 - ln 3}{]} - delim{[}{1/4 - 1/3}{]}](https://www.exampaper.com.sg/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_971.5_f851e925d497efef2879a3bab3e650ff.png)
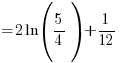
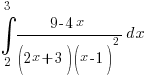 ? 😉
? 😉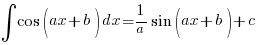
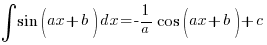
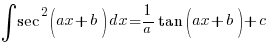
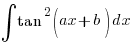
![{}= int{}{}{delim{[}{sec^2 (ax + b) - 1}{]}} dx {}= int{}{}{delim{[}{sec^2 (ax + b) - 1}{]}} dx](https://www.exampaper.com.sg/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_962_b63b4a4fecac09c5a7d3efc25b40425a.png)
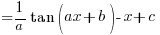
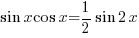 —– (B1)
—– (B1)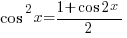 —– (B2)
—– (B2)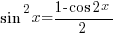 —–(B3)
—–(B3)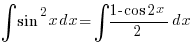
![{} = {1/2} int{}{}{delim{[}{1 - cos 2x}{]}} dx {} = {1/2} int{}{}{delim{[}{1 - cos 2x}{]}} dx](https://www.exampaper.com.sg/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_83b1889235f3bd556ff054b9f075d01a.png)
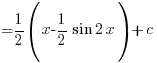
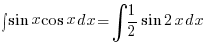
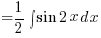
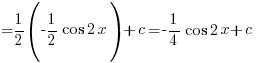
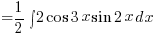
![{} = {1/2}int{}{}{delim{[}{sin 5x - sin x}{]}} dx {} = {1/2}int{}{}{delim{[}{sin 5x - sin x}{]}} dx](https://www.exampaper.com.sg/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_2e791415894fa37022c8dd8c8cb0c4f4.png)
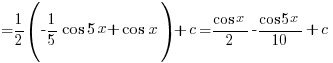
![int{pi/4}{pi/2}{delim{[}{sin^2x - 4 sin x cos x}{]}} dx int{pi/4}{pi/2}{delim{[}{sin^2x - 4 sin x cos x}{]}} dx](https://www.exampaper.com.sg/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_954.5_b4b2624f71bc8b05c18ff80641ee9f48.png)
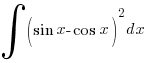
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















5 Comments
曜
日
Integration... me don't like...
It seems you are doing well...
I'm working hard to prepare for math contests...
Cya next year 🙂
曜
日
intergration. oh man.
eeeeeeeeeeeeeeee. lols.
曜
日
We now have evidence that the disdain for Integration is a global phenomenon.
Mgccl: Next year?! Now's only October! What super duper math contests are those? You need to solve for the Meaning of Life?
曜
日
i never understood integration well till i read your notes :p
曜
日
implicit differentiation and subsequently integration ???
Anyway, GC now can help solve very hard differentiation and integration which i struggle in the past
GC roxs =)