Remember me?
The Temple is dark and sad, and tears were shed.
Students with faces as sullen as mine were treasuring their final moments at the sanctuary before setting off for their final mathematical battle of their lives (at least until H1/H2/poly etc.).
and more …
By now, most would have slain and conquered the vile beast known as Additional Mathematics (new 4047 breed) this morning – with records of all lethal blows presented below:
Click the ![]() button and grab it here if you dare …
button and grab it here if you dare …
Access it here if you’re having trouble accessing it on Facebook using your state-of-the-art smartphone 🙁
As usual, please, please leave a comment should you spot any mistake in the solution.
Latest versions:
- 1.0a: Q3(ii) – added explanation of comparing coefficients to clarify how to arrive at 4c = −4, as pointed out by this kind gentleman 😉
Notes from my Mistress:
- Before you ask questions like “I lost x marks in Paper 2, can I still get A1/A2/B3/B4/pass?” or “What is the cutoff for A1/A2/B3/B4/C5/C6/D7/E8/F9 this year?”, please understand that Miss Loi is NOT the Bell Curve Goddess.
- Please also understand that, unless things have changed, there is no half-mark awarded in O-Level Maths. Also it is nigh impossible for ECF if the part involved only carries 1 mark.
So, I can almost “see” you at Halloween on Friday. But it’s more important now to maintain your focus and keep hanging in there, as urged by this student at The Temple:
P.S. And should you need some quick help to get a grip on your remaining papers beyond this most exhausting of weeks, The Temple shall be open this Sunday and next Saturday for your final Social Studies & Chemistry MCQ tune-up respectively.
Remember, remember. Now’s not the time to slip in November!
*begins to crawl out of your monitor screen*







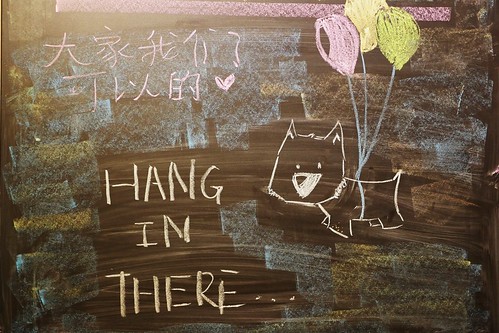



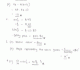

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















22 Comments
曜
日
the answer to Q3 (ii):
12 + c^2 +(4 sqrt3) c = 13 - 4sqrt3
You then equate 4c = -4
why can equate (4 sqrt 3) c = -4sqrt3?
please explain. Thanks
曜
日
@soonek: understood already - by comparing of surd :-))
曜
日
@soonek: Haha was busily moving your comment to the correct blog post when you replied your question 😀
Yes the expression was equated to 4c = −4 via simply comparing the coefficients of the √3 term. Will add this explanation to the workings to clear things up.
Also, for any of you who may be wondering why can't c = ±1 if we had alternatively compared the constants 12 + c² = 13, c cannot be 1 as there is a negative term on the RHS of the expression.
曜
日
Hi I know that this is a dumb question but I was just wondering for question 3ii when you compared the surds,how do you know that (4 sq root 3)= -4 sq root 3? like why not 12+4sq root 3= -4sqrt 3?:o
曜
日
@anon: Umm ... the coefficient of a term refers to a number used to multiply the term, where the term can be a variable like x or a number like √3 in our case.
So when comparing the coefficients of √3 on the LHS & RHS in
12 + c² + 4c√3 = 13 − 4√3
we are only concerned with the multipliers of √3 which are highlighted in red.
曜
日
@Miss Loi: oh ok thanks! so then why can't c²=13 not 12+c²=13? is it because after comparing the coeff of (root3),we are left with 12+c² on the LHS and 13 on the RHS or is there another reason?
曜
日
@anon: Umm ... not exactly ... you can't treat the comparison process like a "cancel on both sides" thingy. Rather, you choose which common terms to compare between LHS & RHS.
In this case, we choose to compare the part on each side of the equation which consists of the constant terms other than the √3 term, as highlighted in red:
12 + c² + 4c√3 = 13 − 4√3
Hint:
Replace √3 with x and treat the above equation as a1 + b1x = a2 + b2x so you are in fact choosing to compare a1 = a2 or b1 = b2.
曜
日
@Miss Loi: Ok I understand now,thank you so much! Truly appreciate it:)
曜
日
@Miss Loi: Why can't 12 + c² + 4c√3 = 13 − 4√3 be factorised like
c²-1+4c√3+4√3=0
(c+1)(c-1)+4√3(c+1)=0
(c+1)(c-1+4√3)=0
c+1=0 or c-1+4√3=0
c=-1 or c=1-4√3?
曜
日
@anon: Yes factorising is fine too ^^
Just remember to reject c = 1 − 4√3 since (2√3 + 1 − 4√3) will give you a negative value for the length of the side of the square.
曜
日
Hi. I have 2 questions. Is it acceptable if:
(1) For question 1, they asked to determine if it was safe to give the food 4 minutes after removal. I found the temperature which was 38.something and I said as after 4 mins it's below 40 so it's okay? Your method was to find the time it took to go below 40, which was interesting.
(2) In the kinematics question, they asked us to prove that the particle would reach P at t = 10 ln 5. Instead of your method I reasoned that at instantaneous rest v must be 0 and so I used t to calculate (to get 0).
曜
日
@Han Quan: For Q1(iii), technically (and with just 2 marks here) you might get away with simply substituting t = 4 into the equation but, with the emphasis of exam questions on application of maths in practical situations these days, Miss Loi feels it's more robust to work this out using the inequality based on the question's condition for the safe temperature of the food to be "less than 40 °C".
This is especially so if you happen to be given a more complex function in which T fluctuates above/below 40 °C as t increases (beyond scope of this discussion).
For Q8(i), again technically you are not wrong to sub t = 10ln5 but with 6 (SIX) marks allocated for this part, Miss Loi suspects they may want to see some e & ln magic from you vs simply v = 0 from a press of your calculator button.
Ultimately, it'll depend on the mark scheme so this is just her own thoughts.
P.S. This seems analogous to the "must I derive or can I just simply substitute the values in the R-formula?" scenario.
曜
日
Hi! For the Kinematics question,I think I misinterpreted it... I thought it was to be show that when T= 10ln5 when particle reaches point P(aka v=0)
曜
日
@Unknown: *points upwards*
曜
日
Hi. Thx for the answer. Will there be pure chemistry(5073) ans??
曜
日
@Anonymous:
曜
日
will you post physcis elective answers??
曜
日
@Amanda:
曜
日
Hello! Will you be posting 5059 physics paper 1 answers for 2014? Thanks 🙂
曜
日
@Anonymous:
曜
日
Will you be able to post the answers to paper 1 of pure biology?
曜
日
@Anonymous: