It’s that time of the year again.
It’s the season when the stifling scent of joss sticks fills the air, and a pall of smoke hangs over the land. A time when little kids are told in no uncertain terms to say ‘excuse me‘ before they go peepee in the bushes.
Shaken by last year’s harrowing encounter with the Binomial Zombie, Miss Loi decided not to stay too late at The Temple tonight, preferring to do up her colourful cutie set of formula sheets within the relative safety of her home this time round.
After a marathon workout session with the laptop, a tired Miss Loi did what most skiving teenagers at her age would do when they take a break from studying: login to her Facebook account.
Sieving through the many dodgy friend requests that invariably showed up, she was drawn to this particular one:
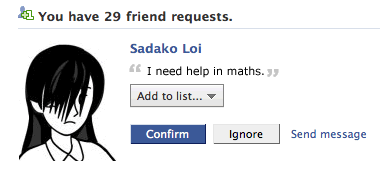
The helpless-looking plea triggered her mathematical maternal instinct, and coupled with her excitement at meeting another Loi, made her click the ‘Confirm’ button without hesitation, totally failing to notice her long unkempt hair, and her Japanese-sounding first name.

A while later this appeared on Miss Loi’s wall

Miss Loi duly replied:
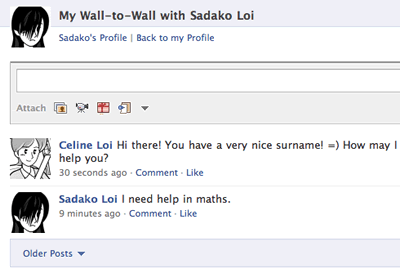
And she replied:
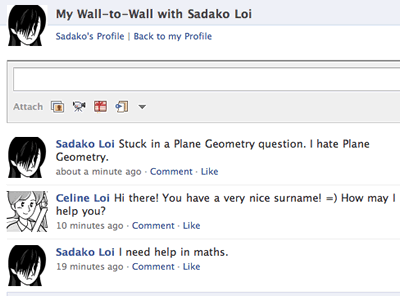
And then Miss Loi replied again:
And finally she replied:
And this was what Miss Loi saw …
At the very moment a stunned Miss Loi finished viewing the video, the Facebook notification icon at the bottom-right of her screen popped up with a message …

… and she found this message waiting for her in her inbox
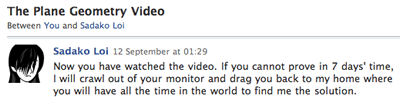
Now that YOU have watched the video, you have seven days to post up the solution here in order to save yourself from being dragged into your monitor screen by Sadako Loi!



 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















19 Comments
曜
日
I'm amazed by your creativity and effort. Speechless Orz..
曜
日
Sigh.. Why in the world did I read this at 2:21am?
曜
日
Die. Have to find solution in 7 days.
曜
日
Now that the three of you have watched this ... 😈
And rinaz, you have even less time since you're technically 6 hours behind.
曜
日
cool, lucky i haven't watch yet. ._.
*closes tab*
曜
日
tohkiat: Think that's why Sadako didn't friend you 😛
3 days have passed ... we're all gonna die ... *sweats*
曜
日
hahahahahahaha sadako has gone back! no need care her alr(:
曜
日
ok miss loi that was hilarious.
曜
日
HI miss Loi, just a random person benefiting from your website. Could you post the solutions to sadaoko's question? i cant realate DM to AB somehow. By the way, how can i improve my maths in 42 days before A levels? I've memorised all my formulae but my results arnt improving much. Should i just chiong TYS for the next 1 month?
曜
日
*Miss Loi's eyes rolls backwards as she looks up suddenly and speaks in a trance-like state*
Nash: Sadako's question isn't easy but word from the netherworld has it that subliminal clues have been planted within that video.
As for your 42-day quest, Miss Loi's finger begins to move towards this link (which should be relevant for A Levels as well)
曜
日
我知道了!!!
Since BE = EC and BM = MC, we can conclude that:
1) triangle BEC is isosceles
angle EBC = angle ECB = x. Hence angle ABE = x since B is 2 times C (given).
And since triangle BEC is isosceles, we can conclude that:
2) triangle BEM is similar to triangle CEM
Since angle EMB + angle EMC = 180 degrees (straight line), and triangle BEM is similar to triangle CEM, so angle EMB = angle EMC = 90 degrees.
3) And thus we can conclude that triangle CEM is similar to triangle CAD (the AAA rule of similarity).
4) sin x = EM/EB (SOH rule)
Ok, proving starts. 😛
Area of triangle ABC = area of triangle ABE + area of triangle EBC.
(1/2)(BC)(AD) = (1/2)(BC)(EM) + (1/2)(AB)(BE)sin x
dividing throughout by 1/2,
(BC)(AD) = (BC)(EM) + (AB)(BE)sin x
substituting sin x = EM/EB,
(BC)(AD) = (BC)(EM) + (AB)(BE)(EM/EB)
cancelling EB in the last term,
(BC)(AD) = (BC)(EM) + (AB)(EM)
factorise,
(BC)(AD) = (EM)(BC+AB)
shifting terms around,
(EM/AD) = (BC)/(BC+AB) -- (1)
By the similar triangles CEM and CAD (proven earlier),
(EM/AD) = (CM/CD)
substituting into equation (1),
(CM/CD) = (BC)/(BC+AB)
shifting terms again,
(BC)(CD) = (CM)(BC+AB)
opening brackets,
(BC)(CD) = (CM)(BC) + (CM)(AB)
re-factorising,
(BC)(CD-CM) = (CM)(AB)
The length of CD - CM is DM (from the diagram given)
substituting,
(BC)(DM) = (CM)(AB)
shifting terms again,
DM = (CM)(AB)/(BC)
The ratio of CM/BC = 1/2 since M is midpoint of BC.
substituting,
DM = 1/2 AB
SHOWN! Ok Sadako Loi stop cursing me with careless mistakes... 🙁
Miss Loi: That's quite a major surgery you have there but basically you've gotten the approach right i.e. prove that EM is perpendicular to BC, set your base angle x and then obtain an expression using the areas of various triangles to finally get your proof!
Did you prove this all by yourself or did you "see" something within that video which somehow subconsciously triggered your inner mathematical prowess? 😉
曜
日
Add on:
2) triangle BEM is similar to triangle CEM (SAS rule)
Hope its clearer. And show that 我没有用猜的。
曜
日
And so if you had watched the video very closely, your subconscious mind will tell you that the key to this supposedly difficult question lies in utilising the areas of triangles (unless someone can think of another approach).
To round this off, here's Miss Loi's (similar) approach, after having her mathematical powers similarly triggered by subliminal messages in the video:
First we try to obtain an expression for DM on the LHS:
As described by mathslover above,
ΔBEC is isosceles
⇒ EM ⊥ BC (M mid-pt. of BC)
⇒ EM // AD
By Intercept Theorem,

 --- (1)
--- (1)
Now there are many ways to utilize the areas of the various triangles to obtain an expression that contains AB for the RHS of the proof (see mathslover's workings for e.g.), Miss Loi shall use the shortest and quickest one here:
Comparing the areas of ΔBCE and ΔABE and expressing them using different formulae:
 (note that they share a common height h)
(note that they share a common height h)
 --- (2)
--- (2)
Sub (2) into (1)


 (MC =
(MC =  BC)
BC)
PROVED!!! *burns a joss stick to Sadako ...*
So may Sadako be appeased by our valiant effort, and hopefully all of you can now add a new weapon (i.e. areas of triangles) from beyond your standard Plane Geometry handbook to your arsenal to fight that hideous Plane Geometry monster!
曜
日
Since when there was intercept theorem?! I went to use similar triangles (and 绕一大圈 to get DM)...
And I didn't see the phantom height h!
There are 3 similar triangles there (BEM, CEM, CAD) and 3 possible variations of sin x ((EM/BE), (EM/CE), part of area of ABE), and it took me ages to figure out which combination will result in terms cancelling each other!
And I even attempted to use double angle (sin 2x = AD/AB = 2 sin x cos x) since it contains the needed line AB.
*kowtows*
Saw the bit at 0.18 by accident, when pausing it to draw the triangle on paper. But it didn't help me the way Sadako intended... I didn't think that much into it...
And saw the other bit after reading your previous post, but the only way I could figure out how to use that information ... is in the lengthy prove. 🙁
曜
日
Knew there was an easier way when I took > 30 mins to solve this supposedly O level question...
and glad that my real Os are long over.
glad that my real Os are long over.
Introducing my ugly handwriting...
http://img40.imageshack.us/i/72643930.jpg/
http://img89.imageshack.us/i/72641804.jpg/
http://img134.imageshack.us/i/16454903.jpg/
Last but not least.. this is fun! 😀
fun! 😀
曜
日
*kowtows to mathslover for your never say die attitude*
辛苦你了 ...
曜
日
Too late.
曜
日
Haha it's still you coz the video is linked to MissLoi's account.
曜
日
By AA test, triangle ABC is similar to triangle AEB
(Angle AEB = 2x = angle ABC, Angle ABE = angle ACB = x)
therefore,
AB/AE=BC/EB = AC/AB
so, AB/AE = BC/EC (given EB=EC)
AB =BC.AE/EC ...(1)
By intercept theorem:
DM/MC = AE/EC ...(2)
subst (2) in (1):
AB = BC.DM/MC
DM = AB.MC/BC = AB/2
cheers.