Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths. Her life's calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over 17 years she has been a savior to countless students ... 
noise pollution in Miss Loi’s estate at 2am
Like Honda’s Type R variant of cars that appeal to Ah Beng racer boys who like to bully weave in front of Miss Loi’s demure little car on the expressways, Trigonometry has its own “Type R” model in the form of the R-Formula that was unveiled in this year’s New AMaths Syllabus.
As such students are warned to listen out for the roar of the R-Formula whenever you encounter a trigonometric question:
-
with an expression that contains a constant, like this:
Solve for 0° < x < 360°,
2 cot x = 3 + 2 cosec x -
or where you’re asked to find an expression’s max/min value, like in this rather cheong hei (long-winded) question:
The diagram shows two right-angled triangles with their right angles at B and N. The sides OB and AB are of length 6 cm and 2 cm respectively. The lines OB is inclined at angle θ to ON. The line AM is perpendicular to ON.
- Express OM in the form OM = R cos (θ + α) and calculate the values of R and α.
- Find the value of θ for which OM = 5 cm.
- In the diagram, state the line with a length of R cm and the angle with a value α.
- Express AM in terms of R and (θ + α) and show that the area of triangle OAM is 10 sin 2(θ + α).
- Given that θ can vary, find the maximum value of the area of triangle OAM and the corresponding value of θ when this occurs.
To handle the new R-Formula questions, students need to recall the following expressions, as they will not be appearing on your formula sheet during your actual exam:
The R-Formula
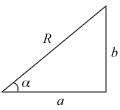
- a cos θ ± b sin θ = R cos (θ ∓ α) - look out for that inverted plus/minus!
- a sin θ ± b cos θ = R sin (θ ± α)
where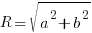 
and 
and a > 0, b > 0, α is acute
Maximum/Minimum Values of R-Formula Expressions
- The maximum value is R which occurs when cos/sin (θ ± α) = 1
- the minimum value -R which occurs when cos/sin (θ ± α) = -1
Deriving The R-Formula
Do note that the R-Formula highlighted above is NOT a given, especially when the relevant part of the question carries a high weightage of marks e.g.
There’s a bit of debate on this but don’t think you can get away with all 6 marks here by simply substituting the values into the R-Formula! So to be a little kiasu, it’s advisable to derive the whole thing as per the following steps:
4 cos θ - 3 sin θ
= R cos (θ+α)
= R [cosθcosα-sinθsinα] (Addition Formula)
= (R cosα)cosθ-(R sinα)sinθ
Comparing coefficients between LHS & RHS,
R cosα = 4 —– (1)
R sinα = 3 —– (2)
(2)/(1): tan α = 3/4 ⇒ α = 36.9°
(1)2+(2)2:
R2cos2α+R2sin2α = 42+32
R2[cos2α+sin2α] = 25 ⇒ R = 5
∴ 4 cos θ - 3 sin θ = 5 cos(θ+36.9°)
Important Notes
To reiterate what was stated above, a and b MUST be positive. DON’T do this:
(-3) cos θ + (-2) sin θ = 3 → WRONG!
Instead, move the terms around to ensure that the first term is always positive:
3 cos θ + 2 sin θ = -3 → CORRECT! YAY!
Please, please, please, please, please for the addition cases (i.e. a cos θ + b sin θ or a sin θ + b cos θ) you can simply re-arrange the sine and cosine terms depending on how you wish to express the R function in your question.
E.g.
3 cos θ + 2 sin θ → if you require R cos (θ - α)
2 sin θ + 3 cos θ → if you require R sin (θ + α)
Hailed as the pinnacle of O-Level Trigonometry, a typical R-Formula question may also require your skills on lesser trigonometry variants such as the Addition Formulae, or the Double Angle Formulae, or the Factor Formulae, together with your knowledge of basic angles (e.g. in question 1 above when you’re asked to find all angles within the range of blah blah blah).
But once you tame it, you’ll be rewarded with a straightforward ride and zoom away with plenty of marks.
So are you ready to test-drive your R-Formula with the two questions above? Miss Loi doesn’t expect you to crash this in your O-Level in two weeks’ time!
*Zooms away for Jφss Sticks Sessions (Type-R variant)*
N.B. Once again, Miss Loi does NOT advocate nor encourage speeding or any form of street racing in Singapore.
Comments
Comments Feed
2 Comments
曜
日
I’m trying this for fun =) (for lbmfh practice actually)
Miss Loi is now marking your answer in a LMBFH manner too
…
1)Is there only 1 answer? My only answer is 247.4
Yes you’re right there’s only one answer! To elaborate, we have
2 cot x = 3 + 2 cosec x
So seeing that lonely constant 3 in the equation should signal to you that you’re going to start the Trigonometry R-Formula engine *VRROOOOOM*
Expanding …
(Note: we put the [2 cos x] as the first term so as to keep a (in the R-Formula) positive)
To express the LHS above in R cos (x + α) form, we have
R = √(22+32) = √13
tan α = 3/2 ⇒ α = 56.3°
(Note: Both a & b has to be > 0 when you’re obtaining α! DON’T do a tan α = -3/2!)
So we now have:
√13 cos (x + 56.3°) = 2
⇒ cos (x + 56.3°) = 2/√13
This is where many students get pwned and forget that All Science Teachers are Crazy (ASTC), as the question asks for ALL values of x in the range of 0° < x < 360°.
So doing a cos-1 2/√13 in your calculator will only yield a basic angle of (x + 56.3°) = 56.3°. But since 2/√13 is positive, we see from the ASTC diagram below that:
⇒ x + 56.3° = 56.3°, 303.7° (1st and 4th quadrant)
⇒ x = 0°, 247.4°
But we shall take only x = 247.4° since 0° is not in the range of 0° < x < 360°!
2)(i)√40cos(θ+18.43)
Once again, to elaborate on your answer (next time show workings okay? Tsk tsk.) …
Typically in a question like this, we first need to express OM in terms of sin θ and cos θ BEFORE we can use the R-Formula. From the following diagram,
… you should be able to see that ∠MAB = θ, and since OM = ON - MN
⇒ OM = 6 cos θ - 2 sin θ
(using your TOA CAH SOH)
Using the R-Formula,
OM = R cos (θ + α) —– (1)
R = √(62+22) = √40
α = tan-1 2/6 = 18.435°
⇒ OM = √40 cos (θ + 18.435°)
(ii)56.2
Think you’ve made a careless mistake here but Miss Loi won’t know in her lifetime the cause of it since your workings are absent!
In anycase, simply equate OM to 5cm and find the value of θ when this occurs:
√40 cos (θ + 18.435°) = 5
cos (θ + 18.4°) = 5/√40
(θ + 18.435°) = 37.761°, 322.239°
Once again don’t forget to A-S-T-C thingy BUT BUT BUT in this case we’re sure from the diagram that θ is acute so we can safely discard the 322.239° and conclude that:
θ = 37.761° - 18.435° = 19.3° when OM = 5cm
(iii)AO, angle AOB
This part requires a bit of 阴阳眼 (The Third Eye) which Anoneemers has demonstrated that he obviously possesses one
You should be able to ’see’ this from the diagram above
(iv)AM=Rsin(θ + α)=√40sin(θ+18.43)
Area of OAM
=(0.5)[√40sin(θ+18.43)][√40cos(θ+18.43)
=20sin(θ+18.43)cos(θ+18.43)
=10sin 2(θ+18.43)
WOAH you have workings now! Yes, from the diagram in Part iii., you can easily see that
AM = R sin (θ+α) —– (2) simple right???
But if you read carefully again, Part iv. only requires you to express in terms of R and (θ+α) (vs Part i. which required you to calculate the values of R and α). So strictly speaking you shouldn’t replace R and α with their actual values in your answer at this point.
Now area of ΔOAM = 0.5 x OM x AM. Using the expressions in (1) and (2),
Area of ΔOAM
= 0.5 x R cos (θ + α) x R sin (θ+α)
= (0.5)R2(0.5) 2 cos (θ + α) sin (θ+α)
(when you see a sine and cosine term with the same angle together - you should instinctively think of the Double Angle Formula for sine!)
Sub in R = √40 obtained from Part i.
= (√402/4) sin 2(θ + α)
= 10 sin 2(θ + α) YAY!
(v)10
Marks are usually served to you on the platter in the Maximum/Minimum parts of R-Formula questions so DON’T EVER 对不起你自己 and skip this part!
From the notes above: The maximum value is R which occurs when cos/sin (θ ± α) = 1.
So in our case the maximum area is simple 10 cm2 (the coefficient of our expression in Part iv) and this occurs when sin 2(θ + α) = 1
⇒ sin 2(θ + 18.435°) = 1
⇒ 2(θ + 18.435°) = 90°
⇒ θ = 26.6° (since θ must be acute)
By the way how do u type all those square roots and teeter symbol i had to copy and paste =.=
It’s my 1st time making
曜
日
Hey Anoneemers, Miss Loi has commented on your test drive of the Trigo R-Formula questions.
Regarding the symbols, Miss Loi was taught from the start to reference this table. But after awhile it became pretty intuitive e.g. for α you type α, for β you type β etc.
But having said that, copy and pasting still seem to be the quickest!
One Trackback
曜
日
[…] admin: […]