As reported previously, Miss Loi has been working late nights (yes, yes, yes you’ll hear about them real soon).

[Source]
When strange sounds were heard coming from the direction of her tummy last night, she finally decided to end the day’s work and drove to the nearest hawker centre (from The Temple, Novena) that was still open at this late hour, for a sinful late night dinner to appease her stomach.
There was barely time to savour the sweet aroma at the smoke-filled hawker centre when she was forcibly promptly ushered by a helper to a table beside a BBQ seafood stall, where rows of tiger prawns were on display and were being advertised at a price of $10 each.
Feeling extremely hungry by now, Miss Loi succumbed to the juicy sight of these succulent prawns. And in a classic don’t-care-3-7-21 (不管三七二十一) rash moment, she decided to throw her entire dieting plan to the wind by ordering a whopping total of FOUR tiger prawns.
Upon completing her messy massacre of the prawns, it was Miss Loi’s turn to be massacred when a bill of $120 was presented to her by the stall owner.
When questioned, the owner shrugged and said
小妹! These are premium prawns! $30 each! Bigger, longer and better than those $10 ones!
Miss Loi, however, was adamant that wasn’t the case.
But they look exactly like the $10 ones.
The owner became agitated.
小妹! WHAT’S YOUR PROBLEM?! LAST TIME WE CHARGE BY WEIGHT AND THOSE *BEEP* ANG MOHS CAME AND GIVE PROBLEM! NOW WE CHARGE BY LENGTH AND A SEXY GIRL LIKE YOU COME AND GIVE PROBLEM!
YOU SAY WE OVERCHARGE YOU – WHERE’S YOUR PROOF?!
With that he took a $10 prawn from the display and placed it, in an oblique manner, beside Miss Loi’s last unfinished prawn on a dish.
NAH! SEE?! YOUR *BEEP* PRAWN IS MUCH LONGER! PROVE IT TO ME IF YOU THINK IT’S NOT!
When Miss Loi tried to align the prawns properly, four well-built men (who looked to be in their 40s) appeared from nowhere and blocked her access to the dish.
OI! *BEEP*! WHO SAY YOU CAN TOUCH?! I ASKED YOU TO PROVE NOT TOUCH!
The prawns, whose lengths are represented by the lines ABC and ADE, are placed in such a way that ABC and ADE are secants of the circular dish as shown in the diagram below.
Given that BC = DE, prove that AB = AD.
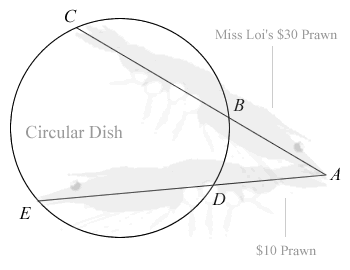
YOU SO SMART YOU COME AND PROVE LAH! *BEEP*! YOU THINK WE HAWKERS GOOD TO BULLY IS IT?! *BEEP*! IF YOU CAN’T PROVE DON’T EXPECT TO LEAVE THIS PLACE TONIGHT! MUAHAHAHAHAHA!!!
*BEEP* *BEEP* *BEEP* *BEEP* *BEEP*
Given that that her 阴阳眼 Of Plane Geometry is refusing to work OT since it’s already late at night, and that this question is similar to an evil tricky one contributed by a student (actually this IS the question, minus the prawns), and that she’s being surrounded by more and more well-built men (who looked to be in their 40s), can you please help Miss Loi (with the aid of the sheet below) prove the above and escape from the hawker centre? 🙁


 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















20 Comments
曜
日
see lah, ask you come eat frog legs you don't want. At least they charge by POT! Wahaahahaha!!
曜
日
幸宰乐祸!!!
曜
日
I want to solve!
Refer to my sketchy un-prawn-like diagram.
[The Un-prawn-like Diagram]
Edit: Sadly, it appears that most Imageshack-hosted images are lost forever 🙁
*strictly there should be modulus sign between each pair 'AB' since it means 'length of AB', but I dunno how to put...*
By the tangent-secant theorem,
CA x BA = (T1A)2 - (1) and EA x DA = (T2A)2 - (2)
Then by the rule of tangents from an external point, since point A is common to both prawns, AT1 = AT2.
Thus equation (2) can be re-written as
EA x DA = (T1A)2
Comparing equations (1) and (2), we can conclude
CA x BA = EA x DA - (3)
Given CBA and EDA are straight lines (actually not given, and prawns don't look straight, but can assume not?), can re-write equation (3) as
(BC + BA) x BA = (ED + DA) x DA - (4)
Given BC = DE, we can re-write equation (4) as
(BC + BA) x BA = (BC + DA) x DA
Comparing both sides of the equation, we can conclude AB = AD.
曜
日
'cher what you say har? I dun unnerstan....
曜
日
When a sexy girl is in danger, a hero will come and save the day! Mr Parallex error, who is infecting those hawker stall assistant with a serious dose of parallex error.
Wahahaha
曜
日
The table at the hawker centre trembled ... and the stall owner & his group of well-built men (who looked to be in their 40s) stared in disbelief as Miss Loi's eyes glowed white from the 阴阳眼 of Plane Geometry sent by mathslover that suddenly descended upon her, as she quickly drew a tangent to the circle from point A as shown in the following diagram:
Actually drawing one tangent (instead of two) will be sufficient, for we can derive the same equations using the Tangent-Secant Theorem with T as a common tangent:
CA × BA = TA2 ----- (1)
EA × DA = TA2 ----- (2)
Note: Don't make the classic Tangent-Secant careless mistake of BC × AB = TA2 or DE × AD = TA2 here! Many students (incl. Miss Loi) had committed this sin in the past 😛
Equating (1) & (2):
AC × AB = AE × AD
When it comes to questions involving the Tangent-Secant Theorem, you'll almost always have to break-up certain terms and to obtain expression in terms of the segments you wish to prove/given in the question.
In this case, we express in terms of BC, DE, AB and AD i.e. all the terms given in the question so ....
(BC + AB) × AB = (DE + AD) × AD
(BC)(AB) + AB2 = (DE)(AD) + AD2
For some reason many students got stuck at this step, as in true Plane Geometry tradition they die die wanted to obtain AB = AD as the final step of their prove. But sometimes life is all about a little bit of flexibility. Since it's given that BC = DE = k
kAB + AB2 = kAD + AD2
And by comparing the LHS and RHS as decreed by mathslover, we prove that AB = AD, and most importantly that both tiger prawns are of the same length!
So what have you got to say now Mr Stall Owner?!
曜
日
Calling all Chinese tutors! There's an assignment available right here on Jφss Sticks! Student's name is FoxTwo! But this one is a problem kid who apparently thinks that 华语 is not Cool!
Ignorantsoup: Unfortunately that stupid superhero Mr Parallax Error seems to be on the wrong side of the table and helping the stall owner who keeps insisting that Miss Loi's prawn is bigger and longer!
曜
日
hey MissLoi :)..y i never learn about this in my add math
曜
日
Actually, you can obtain AB=AD
By the way, my sister is in your class!
曜
日
Welcome to Jφss Sticks rei!!! You probably don't need this in AMaths as the hawkers at your place are nice folks who don't massacre innocent people 😉
曜
日
After being proven wrong, the defeated stall owner and his group of well-built men (who looked to be in their forties) stood speechless and silent as they gathered around Miss Loi's laptop to view Someone's magical factorization workings.
He looked up, with tears streaming down his face ...
With that, the whole lot of them disappeared via 轻功 off the screen.
曜
日
And now, Someone, to the most important thing that holds the key to Miss Loi's state of mind this week ...
Who is your sister?!
*extreme kaypoh mode ON & firing on all cylinders*
曜
日
Ooh Miss Loi has another interrogating case here.
*sneaks out and runs far far*
曜
日
My working correct right? ><
My sister was the one who recently joined your sec4 class, because she was failing her a maths test! She called you herself, after I told her to, around the 1st week of March. From SMSS.
曜
日
Hmm..interesting blog and post. Definitely will come back for more math challenge. Btw, which grade are you teaching?
I am a math lover also, but i never seen this tangent-secant being taught before both in sec school or university. Btw, i am an engineering graduate 😛
Kris
曜
日
Someone: Oops Miss Loi's kaypoh-ness must have gotten the better of her 😛
The wizardry in your factorization working is fine 😉 And for your info, this part actually carries 6 marks in the original question - so it's really open to debate on whether it's required to go beyond comparing the LHS & RHS (which, admittedly, is rather non-routine in an O-Level geometric proof question) just to obtain a final AB=AD, especially in exam conditions.
Actually The Temple has told its students that in an exam, the "best method" for each question shall be the one that enables you to "solve, convince yourself and show the examiner within the required time" i.e. one that acts as a cue to move on quickly to the next question.
Regarding you sis, Miss Loi knows who she is now - the cutie π ballerina with a thousand and one 多姿多采 activities. 😉
曜
日
Welcome to Jφss Sticks Kris! And welcome to the Singapore-Cambridge GCE O Level A-Maths massacre!
曜
日
Yeah! That's her; her name starts with a K. Heehee.
I realized you didn't remove my ( )+... scribblings this time. Yay! It might be a bit strange, but it helps me when checking, and the other required conventional steps are there too.
曜
日
ms loi..huggies (^-^)
曜
日
Hi Miss Loi, I found out a different method to approach this question :x.
Here's my workings.
In Triangle ABD and Triangle ACE,
angle BAD = angle CAE (common)
angle ABD = angle ACE (exterior angle of cyclic quadrilateral)
angle ADB = angle AEC (sum of angles in triangle)
So, triangle ABD and triangle ACE are similar. (AAA similarity)
AB/AC = AD/AE
AB x AE = AC x AD
AB/AD = AC/AE
AB/AD = (AB+BC)/(AD+DE)
AB/AD = (AB+BC)/(AD+BC) - Since DE = BC
AB(AD + BC) = AD(AB + BC)
AB(BC) = AD(BC)
Therefore, AB = AD