Mom and Dad will forever nag about the importance of being a goody two shoes and staying away from shady characters in shady areas. However, the A-Maths Syllabus dictates that every student’s integral-ity be tested by making him/her venture at least once into such areas during the exams. Hur hur hur.
The following question is designed to sieve out the street-smart students from the horribly naive, pampered, and unworldly ones (aren’t we all):
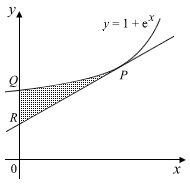The diagram shows part of the curve y = 1 + ex, intersecting the y-axis at Q. The tangent to the curve at the point P(1, 1+e) intersects the y-axis at R.
Find the area of the shaded region PQR.
Upon first glance, many of Miss Loi’s students will go: “Walau! So simple! Just integrate the curve to get the area beneath bounded by the points Q and P, and then integrate the straight line to get the area beneath bounded by the same x-coordinates for points R and P, and then subtract the two areas can already!”.
Miss Loi: “So how are you going to integrate that straight line without knowing its equation?”
Student: *frantically flips textbook for chapters on Differentiation and Coordinate Geometry*
14 Comments
曜
日
Wah your first para is sooooooooo lame...Lol!
曜
日
Winston, you login at 6 in the morning (and risk being late for school) just to say Miss Loi is lame! tsk tsk.
曜
日
I know how students can sometimes be little monsters, but to describe them as unworldly... hmm.
曜
日
Depends on your definition of the word.
From the way we are brought up to the way certain information is 'granted' exposure to the general populace here, can't deny that many of us are 'unworldly', in a certain context of course.
曜
日
It just occured to me, you're the iBook user, aren't you ?
曜
日
Though something Mac-like has made a guest appearance somewhere in this blog, but ... huh?
曜
日
looks like an eqn from my module! ahh i hate that module
not all students are unworldly lar ... some are sweet and cute like me, keke
曜
日
Welcome back encik! Apa kabar?
You are sweet and cute in an 'unworldly' way *lol*
曜
日
dy/dx = m
m = ex
You need to sub in x = 1 before you find the equation of the tangent (straight line) at P. Hence the gradient at P, m = e
equation of line y -(1 + e) = e
^x(x - 1)y = ex + 1
at R, x = 0
with the curve y =e
intergrate curve with x cords with point 1 and 0
and we'll get 2.718
2.718 -( e x 1) - (1/2 x(1 e - 1) x1)
= 2.718 -e - 1/2(e)
= 2.718 - 3/2e
er tats de most i can simply up to-.- whats de ans anyway
= [x + ex]10 - [ (ex2/2) + x]10
= (e/2 - 1) unit2 (after simplification)
曜
日
Hello again Kiroii,
Please see Miss Loi's corrections on your workings! Thanks for your great efforts once more! 😉
曜
日
The calculations are simpler and more elegant if you shift the whole thing down one unit (which doesn't change the area required). Then the tangent touches the curve at (1,e), and since the gradient is trivially e, the tangent will pass through the origin.
The required area is therefore
minus the area of a simple triangle caused by the tangent.
Easier to see with a graph, obviously.
曜
日
@Gavin: Welcome to Jφss Sticks Gavin!
Must say, your approach certainly radiates elegance and is rather brilliant! The gradient of the line being e, together with P(1, e), would straightaway point to the fact that the newly-shifted line passes through the origin - something Miss Loi missed way back in 2007.
Oh why didn't she think of this? WHY DIDN'T SHE THINK OF THIS??!!! WHYYYYY????!!!! *stops her hand from slapping herself*
Alright, the least she could do is present your solution in a proper diagram for the benefit of all:
Thanks for reviving and bringing this old blog post from those carefree days in 2007 back to life 😉
曜
日
Nowadays very care-ful ah?
曜
日
@Johnny Malkacian: o.O ... more like bu-sy these days 😛
Gosh feels like in a time machine right now ...