Chief Stewardess of The HMS Buddha Foot.
Though Miss Loi wished otherwise.
Dear passengers, thank you for sailing with Temple Cruises and welcome aboard the HMS Buddha Foot now departing Bangkok for Singapore. This is your Chief Stewardess Miss Loi speaking.
First of all, a big apology to all passengers transferred here from Flight JS296. Unfortunately as prophesied, the Flight Captain extended his Thai massage timing and now there’s no pilot to fly us back to Singapore. And no way Miss Loi would want to go through another near-death experience with you!
*Nokia ring tone* Oops … excuse me. Yes dear, what’s up?
*unintelligible babble*
You said WHAAAAT????!!! And you want me to tell them that? Ok ok …
I’m terribly, terribly sorry! Our Cruise Captain, with his dashing farang features, has just been ripped off by the farang prices at the harbour fuel station! As such we only have enough fuel to get us stranded in the middle of the South China Sea, where evil pirates plunder unfortunate ships and abduct entire crews of kawaii sailormoon-clad stewardesses!
But fret not! We’ve sent out an SOS an a refueling ship is on her way meet us somewhere to top up our fuel.
Problem is, after spending the whole of last night in some sleazy Bangkok bar, your Captain is not really in the right mathematical frame of mind to calculate where this somewhere might be. This, though, is what he said over the phone:
Our cruise ship is now at the point with position vector (i + 12j) km and is cruising with a velocity of (30i + 20j) km/h.
At this moment, the refueling ship sets off at the point with position vector (85i + 5j), with a velocity of (-50i + kj), where k is a constant.
What must be the value of k in order for the two ships to meet?
Now close the pages of your Passenger’s Handbook as chances are this will not be found there.
Instead, Use the Force, Luke. Trust your feelings. close you eyes and think …
Stuffs like position vectors and i and j indicate to you that this is the other kind of Relative Velocity problem which is solved through vectors.
Compared to the trigonometry kind, this is much easier provided you remember this:
Position vector of an object P at time t, relative to an origin O, traveling at a constant velocity v can be represented by:
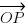+ vt
where 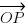represents the initial position of P.
Couple this with your elementary knowledge of column vectors, and you shouldn’t even need to draw a diagram.
So can anyone save the HMS Buddha Foot and her crew of kawaii sailormoons from being stranded in the high seas and becoming a sitting duck for meanies like him?
10 Comments
曜
日
Hello Miss loi, hope you can fave my blog on technorati.
Hope this SOS won't be shared with a Nigerian banker ;p
曜
日
btw miss loi hmm i jus wanna get your comments since my teacher said relative velocity is skipped in some schools as they are difficult to comprehand and should be skipped in the actual exam?
曜
日
Yes there's no denying that relative velocity can strike fear into the hearts of some but for sure at least one question of its kind will appear in your exam (for this year's syllabus).
Moreover they will appear in one of the compulsory questions (i.e. not those either/or kind).
It's fine if you skip this during the exam to do other questions first. But if your school skips teaching this topic entirely doesn't it mean you'll be deprived of the chance to score 7 marks from this?
曜
日
yea well thats what i was telling my teacher-.- he merely said tat it would be left as a low priority chapter and there's hardly any point if we dwell too much into this and most a-maths questions are around 5marks so 7 is no biggie? thats what my teacher zee corpulent pygmy says anyway(ps his nt a fat shortie jus a metaphorical joke)
曜
日
It has been 11 years since I touched A Maths!! Really forgotten what vector calculations are.. but based on my calculations, k = 27 and 19/78 or 27.24 in decimal?? LOL... my answer really look strange.. think sure will fail A-Maths if I take it now.. lol..
btw, I also calculated that ur ship should meet the refuelling ship after travelling 1hr4min, while the refueling one need to travel 1hr2.4min before seeing your? LOL.... Gosh.. I daren't look at weather I'm right or not..
曜
日
Kev, your answer is very, very close but not quite right! Need to see your workings to know where you started to go off-track.
You'll only need very basic column vectors knowledge and two equations to solve this.
But most importantly, don't get distracted by the kawaii stewardess!
P.S. If both ships set off at the same moment, how can they 'meet' at different times???
曜
日
heya! LOL... the sailormoons sure is kawaii neh! Like I say lor.. 11 years never touch A-maths.. all return to teacher liao.. so m using my monkey sense to work this thru... and to answer ur PS, of cos both ships can meet at different times I think. Both ships travel on different velocities would justify meeting at different timing relative to their own starting time.
Ok.. here goes my monkey working..
ur ship is at i, 12j and travelling at 30i + 20j km/h, so after an hour will be at coordinate 31i, 32j. Similarly fuel ship will be at coordinate 35i, (5+k)j after an hour. So, assuming they will meet at coodrinate 33i which is the midpoint (don't think my assumption is true; in fact, they can meet anywhere btw 31i and 35i I think depending on their speed.)
Assuming they meet at 33i, from 31i to 33i, ur ship needs to travel another 2i. 30i + 20j km/h = 2i+1.33j km/4min. So, ur ship will be at coordinate 33i + 33.33j after 1hr 4 min.
For the fuel ship, from 35i to 33i, it needs to travel 2i as well. -50i+kj km/h = -2i+(k/25) km/2.4min. So fuel ship will be at 33i, (5+k+[k/25])j after 1hr 2.4min.
since both have to meet, (5+k+[k/25]) = 33.33
(k+[k/25]) = 28.33
(26k/25) = 28.33 so
k = 27.24
Hmm.. I work backwards using k=27.24, and both ships will meet each other at coordinate 33i, 33.33j. And it seems possible to me that both ships at different speed will take different amount of travelling time to meet each other.
Again these are just my monkey calculations... fire away Miss Loi! =)
曜
日
Oh Kev, this is not a topic on approximation! Tsk.
Instead of assumptions, 'midpoints', 'anywheres', and tediously working backwards, lets talk a bit on position vectors:
You must first understand that both ships lie in the same coordinate plane i.e. i-j plane.
And do you agree that when the ships meet, at time t, their position coordinates (represented by their respective position vectors) are exactly the same?
Let B denote the HMS Buddha Foot and F denote the supply ship,
i.e.
which leads to
So can you form the two equations and get your k from here? 🙂
P.S. Understood your reasoning about the time taken. Yeah one ship could reach the point first and waits for the other.
But but but ... perfect timing is of the essence! The pirates are really active in these areas and we wouldn't want our kawaii stewardess to be abducted while the ship is stuck waiting in the high seas!
曜
日
I may not know how to solve the problem, but let me tell you this: I totally enjoyed the post. And loved the pic too! And I kid you not!
Got here via EastCoast's site. I totally adore the grass design below! Cool!
AnitoKid at http://www.anitokid.blogspot.com
曜
日
Kumusta na pinoy? 🙂
Think most readers like the pic more than the question. Oh well ...
P.S. Does the grass here really looks greener from your end?