Tucked neatly within the (hopefully) crinkled pages of your A-Maths textbook is a little chapter called Binomial Theorem. An innocuous chapter that nevertheless managed to inspire one of the greatest pieces of mathematical working mankind has ever witnessed:
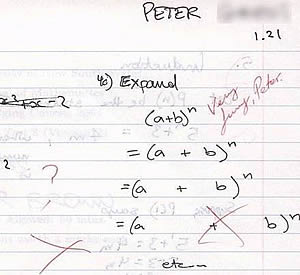
Unfortunately, by this act the great Peter also managed to inspire whole generations of hardcore LMBFH Syndrome suffering students to skip this chapter altogether because it “Looks so difficult! Somemore will only come out once! No time already! Must skip!”.
A pity really, as being one of those *tak glam chapters its questions are usually pretty straightforward, compared to those from its bigger, more glamourous cousins like Functions, Trigonometry, Circular Measure etc. who often have a habit of ganging-up on you.
In fact, Binomial Theorem questions typically only require you to either
- expand an expression OR
- find a specific term in an expansion
So … which kind of question do you think this is?
Given that the expansion of (a+x)(1-2x)n in ascending powers of x is 3- 41x + bx2 + …, find the values of the constants a, n and b.
Now ALL that you need to remember, as far as A-Maths Binomial Theorem goes, is:
(a+b)n = an + nC1an-1b + nC2an-2b2 + … + nCran–rbr + … + nCn-1abn-1 + bn
where nCr =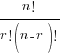 
and the (r+1)th term (Tr+1) of the expansion is highlighted in red.
That’s it. All those labyrinthine pages of unintelligible hieroglyphs in your textbook nicely contained in one cute orange box.
The key to the above question is to know how far to expand the expression, since we’re dealing with an unknown n. For this obvious reason, blur students might be startled to discover that you can’t use the nCr button on your calculator anymore.
In her kindness, Miss Loi shall go further and simplify the three most commonly used nCr expressions for you to remember, so you don’t have to ponder from scratch each time:
nC1 = n
nC2 =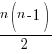 
nC3 =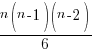 
Now if only Peter had known all these, the world would’ve been a much less interesting place.
*Local colloquial for unglamourous.
30 Comments
曜
日
er im not sure if my ans is correct but
a=3
b= 798
n= 21
曜
日
er wait
a =3
b= -56
n = 7
曜
日
er no wait
b = -266
zz sry for all the mistakes-.- was playing games while solving
曜
日
first i expanded (1-2x)^n
= 1 - 2nx - 2nx^2 (n-1) + ....
for coeff to be 0
it would have to be a x 1 = 3
thus a = 3
for coeff to be x^2
-41x= (1 x X ) + (-2nX x 3)
-41 = 1 - 6n
6n = 42
n = 7
for coeff to be x^2
(-2nX x X) + ( [-2b X^2 (n -1) x a) = bX^2
subing n as 7
b = -266
曜
日
Is that your final answer? *light darkens, Who wants to be a millionaire? music comes on*
曜
日
Kiroii you're treating this as a game show huh? Do you think you'll get 2nd/3rd/4th ... nth chances in your exam? Please ... you need to focus on getting it right the first time.
Let's try this: since you can't edit your own comments, show your workings here and do NOT add another comment to change your answer till Miss Loi has marked it.
This way if you're right congratulations, but if you're wrong then consider you'd just lost the marks in your exam. So be VERY sure before you put your answer here - just like you'll have to be very sure when you write your answers in your actual exam.
FYI, your answers are still not 100% correct. How many terms did you expand to?
BTW EXAMS ROUND THE CORNER AND YOU'LL STILL PLAYING COMPUTER GAMES??!! No wonder always got careless mistakes! Tsk!
曜
日
eh who wants to be a millionaire is outdated-.- its deal or no deal now
曜
日
*bows humbly and grovels
X = the variable x(1 - 2x)n for first three terms
= 1n + nC1(-2x) + nC2(-2x)2
= 1 - 2nx + 4x2 ( [n(n-1)] / 2)
= 1 - 2nx + 2n(n-1)x2 (Simplified for easier reading)
Yes the key here to avoid wasting precious time expanding to more terms than you require. Since the question only gave you up to x2, why do some students still persist to expand beyond x3, x4 ... ? Typical Singaporean kiasu mindset perhaps? Morever the nCr expressions gets more complex the higher you go.
for the coef to x0 to be 3
1 x a = 3
a= 3
Yup in (a+x)(1-2nx+2n(n-1)x2) the only x0 term is (a)(1).
for the coef of x1 to be -41
-41x = (1x) + (-2nxa)
-41x = x - 6nx
6n = 42
n = 7
Yes in (a+x)(1-2nx+2n(n-1)x2) the x1 term is (a)(-2nx) + (x)(1).
for the coef of x2 to be b and subing n to the 2nd and 3rd term of the expansion
(84x2(a)) + (-14x(x)) = b
b = 238( the reason i got negative is due to a careless mistake in expanding sorry..)
(a+x)(1-2nx+2n(n-1)x2) the x2 term is :
(a)2n(n-1)x2 + (x)(-2nx)
= (2an2-2an-2n)x2
So sub in the values of a and n into (2an2-2an-2n), which you did, equate to b and you'll get b = 238.
Simple right? Hope the benign lack of trickery in this topic will encourage students not to skip this chapter.
hmm to be candour im aware of examinations being around the corner but im someone who studies smart and play hard so..i find it explicable that after studying for long hours i should treat myself to some entertainment..
曜
日
er was my previous comment deleted? sigh jus in case it's due to a glitch i'll repost >..< sry for treating it as a game show and spamming (tho unintentional)
曜
日
=.=""? k tis is peculiar i am in a state of disbelief i was thinking my previous comment got deleted then i posted another 1 but my previous comment popped up but my subsequent post is gone >.
曜
日
STOPPPPPP! How many times must Miss Loi remind you there's an active spam filter here that wrongly treats all mathematical workings as 'spam'???
Please wait for Miss Loi to recover your workings from the spam box after you've submitted.
Now she'll have to delete your duplicate comments.
曜
日
-_- oh ok sry sry *grovels further
no seriously sry..din mean it..
曜
日
Hah, WWTBAM is a classic.
曜
日
And so it is.Apart from mathematical workings it already seems as spam 🙁
Discretion is needed.
Winston
曜
日
Aiya, too late cannot b the first to solve :/
曜
日
hohoho~ guess i conceived some commotion>.< anyway miss loi sry fer the trouble i caused
曜
日
Kiroii, ah no worries. Anyway a 'spam filter notice' has been put up below the 'Post Comment' button to inform other commentators who might be in the same situation.
On the contrary, Miss Loi should thank you for actively coming here to solve the maths problems on offer 🙂
曜
日
Winston, are you saying that, minus all the maths workings, Kiroii's comments look spammy?
But on the contrary, Miss Loi didn't find any link or reference to any blog/website/products in all his comments.
According to Wikipedia spamming in blogs is referred to as " ... repeatedly placing comments to various blog posts that provided nothing more than a link to the spammer's commercial web site."
So if we were to follow the logic above, should we then imply that your comment, with two links to your own blog, is a more worthy candidate to be classified as spam? 🙂
曜
日
BR: You just gave Miss Loi an idea for a blog entry based on WWTBAM. Not sure when that will happen though.
123: ah there's always tomorrow, or the day after tomorrow ... No promises yet, but Miss Loi is trying to 'cover' some aspects of all your A-Maths chapters on this blog before the exam starts on the 22nd. Meanwhile, do ask your friends/classmates to drop by and participate in the discussion!
曜
日
😛 I can't deny they seem spammy, but O Levels are coming. Oops the 2nd link i will forgo this time, seeing as I must follow the word of Wily Wikipedia!
曜
日
eh actually from what i see students who are ardent in maths are rather rare >.< even in my class for midyear im the only person who passes in maths-.-""
曜
日
eh actually in my opinion the term "spam" is a butchered word so i wouldnt say winston is wrong nor is he right
曜
日
Kiroii, so late still awake?! Wah...
Anyway it is a butchered word for a definition,but I hope EatYourMaths is not a ...erm... 'repeatedly' 'commercial' blog! 🙁
Haha, now we are indeed having what missli calls possibly-active 'discussion'! 😀
曜
日
I'm Peter...
And THAT was my "expansion"! Cool huh? 🙂
曜
日
OMG are you really Peter the Great?!
If you are indeed the One, you're be permanently inducted into the Jφss Sticks Hall of Fame, and be conferred a special lifetime award in recognition of your contribution to the field of Mathematics!
曜
日
LOL Miss Loi... naw I was kidding, it's not mine... but if it was me, and if I were sweating in the exam hall and staring blankly at this question and have absolutely no idea how to do this question...
Yeah I'd expand it that way...
As I said in a particular shoutbox some time back.... to me, 1+1 = 10, and 11+1 = 100....
*wink*
曜
日
Oh are you one of the foxes? 😀
曜
日
Yup 🙂
I sent you something to your exampaper.com.sg email address... hope you like it 🙂
曜
日
erm 'foxes" and binomal therom was conceived by a person named peter? i though most maths formulas were derived from old maths prodigies
曜
日
Ya Miss Loi is totally correct u lolzz kiroi