It started with a little “oink!” from a student when asked “Who was the former President of the United States?” by his teacher in class.
Appalled by this apparent display of rudeness, the teacher sent the student to stand outside the classroom.
Shocked and puzzled by his dismissal, the sad student cut a forlorn figure outside his classroom, and couldn’t hold back a sneeze at a passing group of giggly girls.
That group of giggly girls giggled at their exclusive naughty joke all the way to the tuckshop, where one of them sneezed while taking her bowl of fish ball noodles from the stall aunty, who in turn sneezed while disposing her stall’s leftovers at the rubbish dump, startling a passing kitten, who in turn let out a BIG KITTY SNEEZE later amidst all the “SOOOOO CUTE!!!” while being caressed by a large gathering of girls, since it was, after all, the school’s resident kitty.

After the dust had settled, the giggles turned into a series of oinks, the kitty spooked everyone with an oink, and students thought the stall aunty was selling bak chor mee.
When certain portions of the school assembly sounded like a pig farm as they sang the National Anthem the following morning, the school principal was sufficiently alarmed to hastily convene a staff meeting, where the Biology HOD stood up and said,
Sir, I have grave news.
Using my lab’s sophisticated equipment, we’ve concluded that the students and the cat have been infected by a new, highly-contagious O1NK strain of the influenza virus.
We believe the first student caught it via contact with Aussie pigs in his Australian Farmstay tour during the school holiday.
As per the H1N1 virus, steps are being taken to set up checkpoints at our school gate. Anyone found to reply “oink” when asked for his/her name will be turned away.
In addition, the following info was obtained from contact tracing:
The school has a total 1500 students. The spread of the virus, since the first student was discovered at Monday 5:00pm is given by
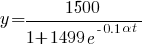 ,
,
where y is the total number of students infected after t hours, and α is obtained by the solution of
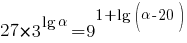
- It’s now 16 hours since the first student first came to school. How many students are infected now (correct to the nearest whole student)?
- Given that announcements are scheduled at the beginning of every hour (e.g. 10:00am, 11:00am etc.), and that according to the Education Ministry’s guideline, the school principal will need to make an announcement to close the school at the hour in which the number of infected students is expected to cross the 45% mark. What time should the principal schedule his announcement?
Unfortunately, the school principal had returned all his math knowledge to his teacher (shame on you!). Hence in order to solve the above problem, he had to rely on his Mathematics HOD, who promptly stood up and said
… OINK!
As part of your AMaths Exponential & Logarithmic Functions chapter, you are almost certain to see in your O-Level exam a question (or part of a question) concerning the application of an exponential or logarithmic function on some scary-looking real-life situations that may involve the likes of a exploding/shrinking population, multiplying bacteria, decaying radioactive substances, cooling temperatures etc.
While the calculation part is usually pretty straightforward i.e. sub the relevant values into the given formula and use what’s stated in Sergeant Loi’s Logarithm Training Program and ln/lg both sides etc., it’s vital that you read the question carefully before submitting your final answer.

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















7 Comments
曜
日
Get a splitting headache whenever I see mathematical equations. My head.... my head....
曜
日
OINK!
曜
日
Kenny: You've returned them all to your math teacher! (Shame on you! 😛 )
Babyface: *Dials 993* *sweats*
曜
日
Miss Loi: Yes in order to proceed with this question, you'll first have to find α from the second equation, and this part requires deft knowledge of the Rules of Indices and the Laws of Logarithms in order to avoid the common pitfalls that have plagued so many ...
→ Yes the numbers 3, 9, 27 at the base are simply crying their hearts out to you to express them in terms of the powers of the common factor 3, in order to 'bring down' the unknown α that's helplessly trapped within the indices (via comparing the indices on both sides).
→ Recall that for the same base, Multiply is to Add: am × an = am+n and Power is to Multiply: (am)n = amn
→ Some students will commit here the usual terrible sin of 2 lg (α − 20) = 2(lg α − lg 20) (WRONG!). Recall your Product Law of Logarithms: loga(xy) then can logax + logay!
→ Recall as well the Power Law of Logarithms: r logax = logaxr that's used here to prepare the lg term on the RHS for the Quotient Law later.
We've successfully reduced the bases to a single 3 on both sides - now we can "bring down" the lg terms by comparing the indices on both sides!
→ Another possible spot for a terrible sin - some students will do a lg α − lg (α − 20)2 = lg (α − (α − 20)2 ) - WRONG! Recall your Quotient Law of Logarithms: logax − logay = loga( )!
)!
→ sadly there're still those who can get stuck at this stage not knowing how to "un-lg/log/ln" their logarithmic/exponential equations. Recall that:
'Un-log': loga y = x ⇔ y = ax
'Un-lg': lg y = x ⇔ y = 10x
'Un-ln': ln y = x ⇔ y = ex
→ Those of you who revise while watching TV may miss out the all-important property of:
.. and get stuck at this point not knowing which value of α to pick from the resulting quadratic equation (Tsk tsk.)
Well and truly written by Someone who obviously doesn't watch TV while revising (Yes?) 😉
With this, we've obtained α = 40 from this beautiful logarithmic equation that requires the entire arsenal of Logarithmic weaponry i.e. basic logarithm properties and the Product Law, Quotient Law, Power Law, as well as the Rules of Indices. Wicked isn't it? 😉
→ So now we move into the first (and typically more straightforward) part of the question, which is simply substituting α=40 andt=16 into the equation. You'll find that e−0.1(40)(16) is very, very small (≈0) hence i.e. the entire school has been infected by the 16th hour.
i.e. the entire school has been infected by the 16th hour.
→ In Part 2, we're finding the value of t when number of infected students crosses the 45% mark. So we begin Part 2 by substituting y = 45% × 1500 = 675 into the equation to obtain t ...
→ and this is the part where you 'ln both sides' to get t out from that e ...
→ and viola! We've found that t=1.78 when 45% of the students gets infected. But this is also the point where many gets a little infected by fatigue after such long and hard calculations that they didn't read the question properly when presenting the final answer. See the Principal's inspiring speech at the next comment...
曜
日
Since the first student was observed at 5.00pm, and that the 45% mark will be breached by 1.78hrs, which is 6:47pm, the announcement will have to be made at the 6pm hour mark.
曜
日
The Principal's voice emerged from a cacophony of "oink oink oink ..." at exactly 6 pm:
*rapturous applause* *throws confetti*
曜
日
Hmm...
I don't watch TV or do anything else when I study. I demand absolute silence... other than the sound of my air conditioner (if I'm in Singapore). You can ask my sister about how particular I am about this...
Anyway, even in the answers of textbooks and stuff, the flooring and ceiling functions aren't used consistently for questions like in the year and related questions; I've been in correspondence with some textbook authors, and supposedly there's no real consensus...
Sorry for the late solution, I was on a self imposed maths exile for 3 months.