It began with a burning sore throat on Sunday, and soon the familiar trigonometry formulae that she was revising with her students began to blur before her eyes.
Despite some students remarking that she was looking like a ghost and probably hoping under their breath that class would end early, Miss Loi managed to finish up the lesson heroically, before canceling classes for the day to rest at home.

桔梗、法半夏、瓜蔞仁、款冬花、遠志、
乾薑、薄荷、蜂蜜 are no match for
the mighty αβ Virus.
Back home, no miracle was forthcoming from the spoonfuls of 京都念慈菴川貝枇杷膏, even though it comes in a lethal blend of 15 herbal ingredients including 川貝、枇杷葉、沙參、茯苓、陳皮、桔梗、法半夏、瓜蔞仁、款冬花、遠志、乾薑、薄荷、蜂蜜 (don’t worry this won’t come out in your exams).
After rolling around in bed for hours, a fever developed. Upon discovering that she had the power to somehow infect her online friends one after another, she decided it was time to visit the neighbourhood doctor to relieve her from her misery.
After rolling around the chair for hours at the clinic (and getting herself exposed to more germs in the process), she finally sat before her doctor who told her in an ominous voice:
My Sexy Maths Tutor, you have been struck by a deadly αβ strain of the flu virus whose roots have mutated into α2 and β2!
The roots of the viral equation 4x2 – x + 36 = 0 are α2 and β2. For the vaccine to cure you, I’ll need to find
- an equation whose roots are
 and
and  ,
, - two distinct equations whose roots are α and β.
Can you help the doctor cure Miss Loi in order to prevent her from infecting and destroying mankind with her virus? *sneeze*
P.S. The events described in this blog post are true, up to the point when the doctor opened his mouth.
With the inclusion of Sum and Product of Roots into Quadratic Equations in the New AMaths Syllabus, you can expect a part or two catering to this topic alongside your usual question on quadratic roots and discriminant i.e. your b2 – 4ac.
While this topic is rather limited in scope i.e. you really only need to know:
For ax2 + bx + c = 0 with roots α, β,
- sum:
 (note the minus sign!)
(note the minus sign!) - product:

and the above equation can be rewritten as:
- x2 – (sum)x + (product) = 0 (note the minus sign AGAIN!)
Do be mindful that the following expressions (which may not be highlighted well enough in your textbook – but you should still be able to derive them easily in times of need) are often needed as well in your calculations:
- α2 + β2 = (α + β)2 – 2αβ
- (α – β)2 = (α + β)2 – 4αβ


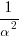 and
and 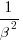 ,
,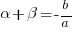
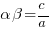
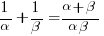

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















10 Comments
曜
日
Umm.... you *did* know I was kidding when I suggested you make a maths problem out of your recent bout with the flu on Plurk, right?
Right?
right?
曜
日
永远支持你。miss loi,miss loi number 1
曜
日
FoxTwo: ... *sneeze*
Piak: Thanks for your fervent support *sneeze*
曜
日
Awww *pat pat* come come I make chicken soup for you....
曜
日
* Miss Loi takes a break from her sneezing *
Part 1












The equation is:
It's interesting that you've chosen to use additional notations i.e. letting α' = α2, Σα' etc. etc.
But to keep to our O-Level scope, we're dealing with quadratic roots (not higher order polynomials) so we're pretty sure that there'll only be two lonely roots α & β (somehow this reminds me of Wall-E & Eve 🙂 )
So for 4x2 - x + 36 = 0 with roots α2, β2:
Sum of roots: ----- (1) (∵
----- (1) (∵  )
) ----- (2) (∵
----- (2) (∵  )
)
Product of roots:
For an equation with roots :
:
Sum of roots:
 using (1), (2) above
using (1), (2) above using (2) above
using (2) above
Product of roots:
So the equation for part 1 is
which can also be expressed as 36x2 - x + 4 = 0 😉
P.S. Someone: These are essentially the same steps you've done but just curious on your choice of notation.
Part 2




This is key part of the working. In their haste, many students have forgotten about this expression α2 + β2 = (α + β)2 - 2αβ when trying to calculate α, β from the given α2, β2 and vice versa!
Actually you already know at this point that αβ cannot be negative - since is obtained from αβ = -3 😉
is obtained from αβ = -3 😉
The 2 equations are:


Once again this can also be expressed as: 2x2 ± 5x + 6 = 0 😉
Pardon me if I have any errors, I'm doing this late at night, and with NO PAPER, using latex as working. Haha
曜
日
By the way, shouldn't:

and the above equation can be rewritten as:
be:
and the above equation can be rewritten as:

since
曜
日
Hi Ms Loi, take care and get well soon! 🙂
曜
日
Haha. My choice of notation is from the all powerful Bostock and Chandler. Heehee. Yay! I got it correct. Woot.
曜
日
I prefer to use




because it helps me to remember the general form of Vieta's forumulas
when you sum , you take the next letter b (taking alpha as the letter a), with a minus sign in front BECAUSE its an ODD number of roots, getting
, you take the next letter b (taking alpha as the letter a), with a minus sign in front BECAUSE its an ODD number of roots, getting 
when you sum , you take the next letter c (taking beta as letter b), without any minus sign in front BECAUSE its an EVEN number of roots getting
, you take the next letter c (taking beta as letter b), without any minus sign in front BECAUSE its an EVEN number of roots getting 
曜
日
And so it came to pass that on a historic weekend when The Temple reverberated with the sounds of roaring F1 cars, Miss Loi was finally healed by a potent vaccine that was concocted by Someone, using ingredients from an A-Level 武林密籍 that overwhelmingly killed the virus in an instant.
P.S. O-Level students are advised not to be alarmed by the chim concepts presented in Comment #9, for you'll ONLY be dealing with two roots in your exam - so just focus on the stuff in the orange boxes within the main blog post.
P.P.S. The typo mentioned in Comment #6 has been fixed. Miss Loi was really sick when she put out this blog post (yeah yeah excuses excuses ...)
Last but not least, thanks FoxTwo and Daniel for pats pats and your well-wishes. The sneezing has completely stopped now 😀