To the Mathematics aristocrats who feel that questions here are getting “so easy, my grandma can do it!“: It’s now crunchtime for the O-Levels, not the Maths Olympiad. Time to forget that killer prelim paper from your elite school. Instead, it’s time to focus on getting that distinction by simply answering more standard TYS questions correctly than 75% of your cohort.
Though modern science has shown that Singaporean math students are the best in the world, the O-Levels are really just a collection of standard questions for the vast global student population. And to many, these seemingly easy questions could be cases of “so difficult, my grandma will kill me!“.
Instead, more pressing are the massive, massive numbers of careless mistakes tragically commited by students each year. That’s where Miss Loi comes in now – to nag you to death forewarn you of all the age-old traps that might lead to your downfall.
Take for instance this scheming pair that have been recently appearing side-by-side in your TYS:
- Find the range of values of x for which (1-3x)(x+2) ≤ 4.
- Find the range of values of p for which x2 – (p + 3)x + 2p + 3 > 0 for all values of x.
Note that one asks for the range of x while the other asks for the range of p. Miss Loi shall give it all away by revealing one requires you to find the discriminant while the other requires the roots. But both parts look so similar. So which is which?
Shouldn’t be a problem for the aristocrats and their grandmas, but for the rest of the grandmas out there the Quadratic Equations chapter can be a long and confusing one with all those sexy curves that naughty male students never fail to make jokes of. Tsk.
In any case, Miss Loi shall be nice by providing this chart that will hopefully refresh all grandmas’ ageing memories:
| Discriminant b2-4ac | f(x) = (x–α)(x–β) |
|---|---|
| > 0 |  |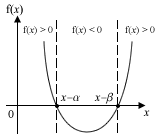
| = 0 |  |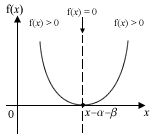
| < 0 |  |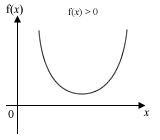
Now go for it Granny Power!
20 Comments
曜
日
1) 3< x < -2/3 ( < is greater or equal)
2) cant do metally so lata>.>
曜
日
eh for 2nd i 4got abt the way discriminate should go>.
曜
日
gahh zz here comes the error
uh b^2 - 4ac < 0
(p-3) (p+1 ) < 0
im guessing it should be
3< p < -1
曜
日
Kiroii,
Miss Loi made a typo in Part 1 of the question (should be (1-3x)(x+2) ≤ 4). Just changed it, so could you retry this part (with workings) please? See, Miss Loi's also not immune to careless mistakes 😛
For part 2, you're looking for the range of p which actually constitutes the coefficients of x2, x etc ... so this is the cue that you're gonna deal with the discriminant. Hence for the entire expression to be > 0 for all values of x (i.e. the entire curve must be above the x-axis), it's discriminant must be < 0, from the table given.
So you're right and you managed to factorize and obtain the values of p at either end of the range.
BUT YOUR FINAL ANSWER IS TRAGIC! How can any number be < -1 and > 3?????
曜
日
juz coz you said please~
after expanding
-3x^2 - 5x +2 ≤ 4
( < refers to greater or equalto)Next time try using ≤ or ≥0 ≤ 3x^2 + 5x + 2
0 ≤ (3x + 2) (x+1)
-2/3 ≤ x ≤ -1
Yes you rightly looked for the roots of the expression when finding the range of x. You got your roots right but if you're confused for the range, it's always safe to quickly sketch out the curve for your obtained expression 0 ≤ (3x+2) (x+1) ≥ 0. Since the coefficient of x2 is positive, the curve should be a valley like this:
You're looking for the range of values of x for which (3x+2) (x+1) ≥ 0. So from the diagram, it's clear you should be looking at the parts of the curve above the horizontal zero line (the shaded areas). So shouldn't your range be x ≤ -1 and x ≥ -2/3?
as for 2 uh it's an imaginary curve yes? but i have never encountered a question where there are 2 values..usually 1 value..so i have no clue as to which way is which i was thinking
+| - | + so>.
Similarly for part 2, you're looking for the range of values of p for which (p-3) (p+1) < 0. So sketching out the curve again (once again it's a valley coz the coefficient of p2 is positive):
This time you're looking for the range of values of p for which (p-3) (p+1) < 0. So from the diagram you should be looking at the part of the curve below the horizontal zero line (shaded area). So you range should be -1 < p < 3 ... which is logical.
So to avoid careless mistakes and confusion when finding range of values in your exam, a simple quick sketch can do wonders in making things clearer. Just don't make wild guesses coz chances are you guesses will be wrong!
曜
日
oh yea juz outta curiousity miss celine loi ya familar with history? o lvl syl of coz
曜
日
Kiroii, just marked your workings and answers.
History? As in the years of the different LV collections? 😀
曜
日
i dun get it... For part 2, why is the discriminant less than 0?
曜
日
123,
Read part 2 carefully. It says x2 - (p + 3)x + 2p + 3 > 0 for all values of x.
What does this mean? It means the expression is always positive ⇒ the entire quadratic curve lies above the x-axis. And since it will never ever cut the x-axis ⇒ this curve has no real roots.
And since the coefficient of x2 is positive, which scenario do you think this refers to in the table above which Miss Loi had painstakingly drawn up?
曜
日
eh but i dun get it why is an imaginary curve the area which is looking for is as you mentioned cant it be the same as part 1? and btw i was under the impression o lvls imaginary curves are rather elusive?
and hist i dun mean LV collections>.< i ment "hail hitler" tat sorrta thingy anyway sent ya somemore questions-_-
曜
日
No it can't be the same as part 1.
Let's summarize:
In part 1, we have (3x + 2) (x+1) ≥ 0 so we're looking at the portion(s) of the curve above the zero line (i.e. x-axis).
In part 2, we have (p-3) (p+1) < 0 so we're looking at the portion of the curve below the zero line.
BTW Miss Loi is curious as to what's your definition of "imaginary curves"?
As for history, Miss Loi can only "hail LV/Gucci/Prada", unfortunately.
曜
日
uh RIGHT the < symbol ..
er imaginary curves = discriminant
it's whats written in my textbook >.< and i find it more apt then discriminant as this kinda curves are rather "stupid" ?
as fer history>.
曜
日
i din noe that tution teachers command salaries enough for such stuff?
曜
日
Miss Loi only said "hail", as in "worship". Didn't say 'buy' 😛
曜
日
Hi, kirroi. I am a fellow History Elective student too. What essay questions does your history teacher feels that will appear this year? My teacher has a sudden premonition that Japan/ Reasons for WWII will come out for section B, while China(1967-1989) will come our for Section A.
曜
日
huh reasons for ww2? dunno my teacher juz told us to focus on china, germany and russia esp germany comes out yearly but nonetheless i memorised the whole book btw im a pure hist student
曜
日
btw china from 1967 ya mean china after mao? if im nt wrong smthin like china after ww2 came out fror a lvls last year
曜
日
eh btw miss loi dun hail/ worship till becoming the idiom penny wise pound foolish by turning into a compulsive gucci must have tai tai~
曜
日
If you've read the About Miss Loi page, you'd find that she's already trying her very best in "preparing for her eventual tai tai lifestyle". But for the moment there's still a long way to go ...
BTW guys, is there a Jφss Sticks for History somewhere on the net where you can discuss this?
曜
日
>.< miss loi is kickin history aficionados out tats mean LOL