In this critical part of the year, The Temple resembles a ‘United Nations’ of sorts – a mass gathering of chatty students representing the many schools of Singapore, coming together for a common cause as one united people, regardless of race, language or religion, so as to achieve their A1s and happiness and avoid scoldings by teachers and parents.
It’s also the period when the number of extra lessons increases, along with the probability of students from one class meeting those from another.
Take Student J and Student T for example, two conscientious, single & available, hot-blooded boys who had been diligently attending Miss Loi’s joss sticks sessions since time immemorial, who were eagerly anticipating their next class – one that was rumoured to have many chio girls in attendance.
Imagine their dismay when it turned out to be an all-boys’ class, with Miss Loi being the chio-est girl in the class.

As they swallowed their bitter disappointment and resigned themselves to the mundane maths questions on their desk, a crumpled piece of paper flew out suddenly from nowhere to hit them on the head.
Startled, they turned towards the direction of the missile, only to find their jaws dropping simultaneously at the sight of an absolute stunner of a girl, dressed in the most kawaii Sailormoon uniform, seated at the far corner of the room.
The long, flowing Pantene hair, an impish smile, and a wink from the almond-shaped eye of this suspected Japanese exchange student were all it took to divert their attention firmly away from the quadratic curves on the board to the curves of her slender body.
They were desperate to stem the bleeding from their noses now, as she pointed her finger teasingly to the crumpled pieces of paper on the floor, which they hastily picked up to discover the following message scribbled inside:
Hello Handsome!
Maths is soooo boring! I’m falling asleep! Can you please pass me some Sour Sweets from the jars on your desk?
The one who passes me the most Sour sweets will get a date with me tonight *wink*
And thus, as hot-blooded males in heat tend to do in these situations, they promptly discarded their BFF status and began grabbing sweets frantically from the jars, totally oblivious to the fact that, to the rest of the people in the class who couldn’t see this girl, Miss Loi was still the chio-est girl in the room.
Two jars containing a mixture of Sour and Cola sweets lie before Students J and T respectively.
As of now, both of them had made three failed attempts to pass sweets to the girl, for they were caught by Miss Loi each time they grabbed a handful of sweets from the jars (students at The Temple are allowed one sweet at a time for their own consumption only). All sweets taken from the jars were confiscated and never placed back into the jars.
The tables below show the number of sweets in each jar at the beginning, and the number of sweets taken out and confiscated by Miss Loi on each attempt.
| Student J | Student T | |||
|---|---|---|---|---|
| Sweet Flavour | Sour | Cola | Sour | Cola |
| Total in jar at the start | 40 | 25 | 24 | 48 |
| 1st Attempt | 14 | 18 | 4 | 10 |
| 2nd Attempt | 10 | 0 | 12 | 22 |
| 3rd Attempt | 4 | 2 | 6 | 6 |
Given that the number of sweets Student J has taken out on his three attempts is represented by the matrix M = 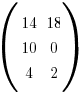 , and that the same information for Student T is represented by a matrix N.
, and that the same information for Student T is represented by a matrix N.
- Write down the matrix N.
- Given that L =
 , calculate J=LM and T=LN. Describe what is represented by the elements of J and T.
, calculate J=LM and T=LN. Describe what is represented by the elements of J and T. - Calculate K=L(M+N), and describe what is represented by the elements of K.
- Calculate
 − K, and describe what is represented by the elements of
− K, and describe what is represented by the elements of  − K.
− K. - If they both managed to take out all the remaining sweets from the jars and pass them all to the girl on the 4th attempt (due to Miss Loi being in the toilet), by comparing the relevant elements of two suitable matrices, determine who gets to ‘date’ the girl.
- A Sour Sweet costs $0.60 and a Cola Sweet costs $0.40. Write down two matrices such that the elements of their product under matrix multiplication will give the total cost of the sweets in each jar. Hence, find the total cost of the sweets in each jar.
Hope this cheong hei (ala long-winded) question will provide some practice on Matrix Addition/Subtraction/Multiplication in an Application of Matrices in Solving Everyday Life Problems for those of you studying for your O-Level EMaths now, though it’s not everyday you get the chance to go on a date with Sadako a pretty girl!

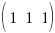 , calculate J=LM and T=LN. Describe what is represented by the elements of J and T.
, calculate J=LM and T=LN. Describe what is represented by the elements of J and T.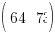 − K, and describe what is represented by the elements of
− K, and describe what is represented by the elements of 



 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















7 Comments
曜
日
Cant draw matrices on this thing so please bear with it..
Miss Loi: Commencing conversion of your matrices into a more readable form ...
1) = N
= N
Yes. Since M has been defined as a 3x2 matrix for the sweets Student J has taken (the blue numbers in the table), we read off the relevant rows and columns for the matrix N for Student T (the green numbers in the table):
Note that data in the first row (with info on the total sweets in the jars) to not used to form the matrix in this part. Please always read such long-winded questions carefully to avoid reading off the wrong rows/columns.
2)
J =
Yes, J=LM as defined in the question.
So via a straightforward matrix multiplication,


J =
=
=
T =
Similarly, T=LN


=
=
=
Matrices J and T shows the total no. of cola and sour sweets taken by students J and T ( and confiscated by Miss Loi)
Yes. From the table in the question, you'll see that J and T represents the total no. of sour (left column) and cola (right column) sweets taken out from each jar in the three attempts.
3) The inter-mediate step are too hard to type for this part so ill just give the final answers.
K = (50
5458) → No workings leads to careless mistake! 😡K=L(M+N)![(matrix{1}{3}{1 1 1})delim{[}{(matrix{3}{2}{14 18 10 0 4 2})+(matrix{3}{2}{4 10 12 22 6 6})}{]} (matrix{1}{3}{1 1 1})delim{[}{(matrix{3}{2}{14 18 10 0 4 2})+(matrix{3}{2}{4 10 12 22 6 6})}{]}](data:image/svg+xml,%3Csvg%20xmlns=%22http://www.w3.org/2000/svg%22%20viewBox=%220%200%20210%20140%22%3E%3C/svg%3E)



=
=
=
=
OR if you trust your own answers and feelings from Part 2 ...
Since matrix multiplications are distributive (basically this cheem term, if you recall from Sec One, means A(B+C) = AB+AC),
K=L(M+N) = LM+LN

= J+T (from part 2)
=
=
And since K = J+T, it represents the total no. of sour (left column) and cola (right column) sweets taken out from both jars in the three attempts.
4) (64 73) - (50
5458) = (141915)→ careless mistake cascaded from Part 3 😡
(14
1915) represents the no. of cola and sour sweets left in the jarsSuddenly, an alien matrix with two alien numbers (64 and 73) not found in the table hovers in the question to strike fears into us earthlings.
But if you stop and take a deep breath, you'll realize that we're trying to subtract K, which is the total no. of sweets taken from both jars, from this alien matrix. As such, we may instinctively deduce that this matrix must have something to do with some total amount with elements that are greater than the respective ones in K, since we shouldn't have any negative elements here.
So we look to the row of data that hasn't yet been utilized in this question ...
And viola ... 40+24=64 (total no. of sour sweets in both jars) and 25+48=73 (total no. of cola sweets in both jars)!
⇒ (64 73) − (50 58) = (14 15) ⇒ the no. of cola and sour sweets left in the jars
5)
Total no. of sweets given to the girl by J
= 40 + 25 - 14 - 10 - 4 - 18 - 2
=17
Total no. of sweets given to the girl by T
= 24 +48 -12 - 4 - 6 - 6 - 22 -10
=12
Since student J gave more sweets to Sadako than student T, J get the right to date Sadako. Good luck with that ^_^''
And so we come to the dreaded part in EMath matrix questions that requires you to form your own matrices.
We wish to know how many sweets (specifically Sour sweets) that was passed to the girl by Students J & T in the final round. Mathematically speaking it's simply:
From Part 2, we already have J & T representing the total sweets left in each jar after 3 attempts.
And if one were open one's eyes big big the total no. of sweets at the start is staring at you in the face from the first row of the table:
So we can form and compare our matrices as follows:
(40 25) − J
= (40 25) − (28 20)
= (12 5)
(24 48) − T
= (24 49) − (22 38)
= (2 10)
And since Sadako loves Sour sweets in the story (ok should've included this in the question proper), we compare the left column of each matrix to find Student J has given more Sour sweets (12 vs 2) to 'win' her heart!
5)
(0.6)
(0.4) = X
Cost of sweets = (64 73)X [must be multiplied in this order]
=$67.60
Again, we say this aloud:
Total cost of sweets in each jar
= Cost per sweet × Total no. of sweets in jar OR
= Total no. of sweets in jar × Cost per sweet
Once you've confirmed to yourself that the above statement makes sense, you go about 'creating' your matrices:
Cost per sweet:
 OR
OR 
Total no. of sweets in jar:
 OR
OR 
So which matrix do you use for your product expression? IT DOESN'T MATTER as long as multiplication is possible (i.e. no. of cols in left matrix = no. of rows in right matrix) AND make sure you check that you're multiplying the right elements.
So, say, should you einee menee minee mo and select and
and  and you put them in this order:
and you put them in this order:
⇒ FAIL
But if you switch them around:
=
(CHECK that you're multiplying 0.60 with Sour sweets and 0.40 with Cola sweets!)
=
⇒ YAY!
On the other hand, if you einee menee minee mo again and select and
and  you can get lucky if you put them in this order:
you can get lucky if you put them in this order:
=
(CHECK again that you're multiplying 0.60 with Sour sweets and 0.40 with Cola sweets!)
=
⇒ DOUBLE YAY!
You're get the same final answer but note that the order of the final matrix is different!
Hopefully Sadako will let me go for not solving the triangle question now o_o...Thanks in advance Miss Loi, I am not IT savvy enough to put matrices in my post
曜
日
Oh by the way Miss Loi, The maths department at my school (the video) comes up with whacky stuff only once in awhile its not really all fun and games there ^_^''
曜
日
Nash: Just completed the loooong marking of your workings.
Take heart that while wordy EMaths matrices questions tend to be a little, well, wordy, the underlying mathematics is usually very straightforward as (in the absence of AMaths stuff like determinants and inverse matrices) there's really nothing much they can ask in EMaths matrices, one simply has to do a bit of reading comprehension to understand the question fully before barging in.
P.S. It's not that difficult to 'draw' matrices in your comments (imagine even an IT-inept Miss Loi can do this!)
Refer to the syntax guide and you'll find this:
e.g. [ pmath ](matrix{row}{col}{1 2 ... elements})[ /pmath ].
Try it using the preview button below 😉
曜
日
Oh and, as some students would know, it's not really all fun and games at The Temple either.
*shows stern face*
曜
日
Hi Handsome Nash!
So sweet of you to solve the question!
Suddenly I don't feel like going out with T or J anymore. I wanna go out with you!
*wink*
曜
日
Sorry Miss Loi, I will be more careful for future posts and my upcoming exams (bows head) and i will also learn syntex to make life easier for you.
It hurts more to be scolded by a person you never even see b4 (looks at censored sunday time paper) >_<
To Sadako
I don't mind, a ghost buddy will be useful when i go to Tekong in Feb. but come find me in Dec, AFTER my exams.
Bet u didn't expect that =P
曜
日
Nash, Miss Loi got scold you meh???
Sadako! Leave the NS boy alone! Shoo! Shoo!