As the first day of Chinese New Year draws to a close, terrifying news have been coming in from all corners of the land.

With Judgement Day falling before Chinese New Year for the first time in living memory, a second “Judgement Day” took place today, as an entire nation of post O-Level students stood in line to be ruthlessly massacred by gossipy relatives thirsty for the blood of their O Level results, JC/Poly choices, singlehood status, IQ level, height and weight, amongst other things.
Escaping today’s carnage only because her house-visiting starts on the second day of CNY, a particular Student now dreads the prospects of facing her three aunties tomorrow i.e. a Gossipy Aunty who likes to compare her son’s exam results with hers, a Kaypoh Aunty who likes to ask if she has a boyfriend, and a very mean Evil Aunty who always say that she “has put on weight compared to last year”, even though her weighing machine showed exactly the same reading year after year.
Having just broken up with her two-timing boyfriend and still anxious of where she’ll end up on Friday, she really fears that her festive season will be ruined by people whom she only meets once a year.
As such, she wishes to find out her odds of survival tomorrow …
Analyzing the historical data of her past visits, there’s a 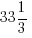 % chance of running into Gossipy Aunty A, a 25% chance of running into Kaypoh Aunty B and a
% chance of running into Gossipy Aunty A, a 25% chance of running into Kaypoh Aunty B and a 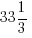 % chance of running into Evil Aunty C in a particular house visit.
% chance of running into Evil Aunty C in a particular house visit.
- The *probabilities of Gossipy Aunty A asking about her O Level results, asking which JC/Poly she’s going, and showing-off her son’s results are
 ,
,  and
and  respectively.
respectively. - The *probabilities of Kaypoh Aunty B asking about her O Level results, asking which JC/Poly she’s going, and asking if she has a boyfriend are
 ,
,  and
and  respectively.
respectively. - The *probabilities of Evil Aunty C asking about her O Level results, asking which JC/Poly she’s going, and pointing out that she has gained weight are
 ,
,  and
and  respectively.
respectively.
Given that each aunty only gets the chance to interrogate/scrutinize her once when they meet, and that there’s absolutely no chance of running into more than one aunty during her visit (∵ they hate each other to the core due to some conflict in their past lives), calculate the probability of her
- being asked about her O Level results.
- being asked about her O Level results or the JC/Poly she’s going.
- escaping any questioning/scrutinizing during the visit.
If she has to make a total of three house visits during this Chinese New Year, and that the probabilities are exactly the same as those described above for each visit, find, correct to 3 significant figures, the probability of her
- escaping any questioning/scrutinizing in at least two visits.
- having a happy Chinese New Year (i.e. avoiding any questioning/scrutinizing on all three visits)
At this point, she realized to her dismay that the carefree months following her O Levels have caused her to generously return all her knowledge of EMaths Probability to her Cher, but she still have a vague memory of her sexy maths tutor saying something to the effort of
For this kind of cheong hei long-winded Probabilty question, it’s important that you draw a Probability Tree Diagram to help you see clearly ALL possible outcomes in the scenario.
Can you help our Student find out if she’s going to have a Happy Chinese New Year tomorrow?

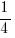 ,
, 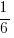 and
and 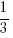 respectively.
respectively.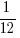 and
and 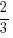 respectively.
respectively.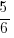 respectively.
respectively.

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















5 Comments
曜
日
PART 1
1. P(being asked about her O Level results) = 1/3 * 1/4 + 1/4 * 1/6 + 1/3 * 1/12 = 11/72
Miss Loi: Yup this is simple.
Since it's been stated that there's no chance of running into more than one aunty during her visit, and that each Aunty can ask her only one question when our Student runs into her,
i.e. Mutually exclusive events = when Event A occurs, then there's absolutely ZERO chance of Event B occurring.
So the only possibilities of our Student being asked about her O Level results,
P(asked O Level results) =

P(Run into Aunty A) AND P(Aunty A asks O Level results) OR
P(Run into Aunty B) AND P(Aunty B asks O Level results) OR
P(Run into Aunty C) AND P(Aunty C asks O Level results)
N.B. EMaths Probability calculations are usually % chance of running into Aunty B" - which you should instantly laugh into his face and say "Nah
% chance of running into Aunty B" - which you should instantly laugh into his face and say "Nah  just say
just say  lah!"
lah!"
prettyvery straightforward. Often, an evil examiner's only recourse to 'challenge' you is via 'confusing' you with phrases like "2. P(being asked about her O Level results or the JC/Poly she’s going) = 1/3 * (1/4 + 1/6) + 1/4 * (1/6 + 1/12) + 1/3 * (1/12 + 1/12) = 37/144
Yup - continuing with the same reasoning in Part 1,
P(asked O Level results OR JC/Poly choice) =

P(asked O Level results) OR P(asked JC/Poly choice)
P(asked O Level results) OR
P(Run into Aunty A) AND P(Aunty A asks JC/Poly choice) OR
P(Run into Aunty B) AND P(Aunty B asks JC/Poly choice) OR
P(Run into Aunty C) AND P(Aunty C asks JC/Poly choice)
N.B. Different workings but same answer!
3. P(escaping any questioning/scrutinizing during the visit) = 1 - 1/3 - 1/4 - 1/3 = 1/12
*Deng deng deng deng* ... unfortunately in a longish story-telling question like this, the euphoria one experiences from the relatively-straightforward earlier parts usually precedes something more sinister in the later parts. In this instance, there can be a limit of how far one can go, in terms of accuracy, when attempting Probability questions without the aid of a diagram:
While Miss Loi said earlier that EMaths Probability calculations are straightforward, the real challenge usually lies in the extraction of information from the question, as well as deducing what the question doesn't tell you. In this case, it's often about
Looking at the RED portion of the Probability Tree Diagram above, besides the case of not running into any Aunty, it's obvious there are another two cases when the Student can escape questioning i.e. when Aunty A or Aunty B keeps quiet after meeting the Student.
So P(escape questioning/scrutinizing) =

P(not running into any Aunty) OR
P(Run into Aunty A) AND P(Aunty A keeps quiet) OR
P(Run into Aunty B) AND P(Aunty B keeps quiet)
Hence a quick sketch of a Probability Tree Diagram (even when not asked) in your exam can be invaluable in helping you to see at a glance ALL possible outcomes and ensure that you don't miss out any. Also, in the event of a chorus of complaints/protests in the likes of "the question not phrased properly lah", "question not clear lah" ... it's worth noting that the sum of all probabilities branching out from each node must be 1.
So alarm bells should be ringing when you check that the given in the question for Aunty A, and the
given in the question for Aunty A, and the  given for Aunty A, aren't equal to 1. Aunty C is really evil and mean as
given for Aunty A, aren't equal to 1. Aunty C is really evil and mean as  ⇒ she'll die die question/scrutinize our Student if she unfortunately runs into her 😛
⇒ she'll die die question/scrutinize our Student if she unfortunately runs into her 😛
PART 2
1. P(escaping any questioning/scrutinizing in at least two visits) = 1/12 * 1/12 * 11/12 * 3 + 1/12 * 1/12 * 1/12 = 0.197
You've correctly covered all the cases for P(escaping any questioning/scrutinizing in ≥ 2 visits) but unfortunately your final answer is affected by the value of P(escape questioning/scrutinizing) you've obtained in Part 1.
From Part 1, we've obtained
P(she'll be asked/scrutinized on a visit) =
Since she can only either escape or fail to escape being asked/scrutinized on each visit (i.e. these are the only two possible outcomes for each visit),
⇒ P(she'll NOT be asked/scrutinized on a visit) =
To make things a bit clearer, here's a second Probability Tree Diagram for the three house visits in Part 2:
From the diagram, we can easily see that for P(escaping any questioning/scrutinizing in ≥2 visits), there're only the following 'paths' that she can take:
∴ P(escaping any questioning/scrutinizing in ≥2 visits)




2. P(having a happy Chinese New Year) = 1/12 * 1/12 * 1/12 = 0.000579
Following what's described above, P(having a happy Chinese New Year) should then be
Hee... So the student probably can't have a very CNY after all....
Yes a CNY to forget indeed. Poor thing. 🙁
曜
日
Welcome to Jφss Sticks Jacelyn and thanks for helping out our poor heartbroken Student!
Miss Loi has marked and commented on your workings and, upon seeing her bleak probabilities, the Student sincerely hopes that all the kaypoh gossipy aunties in the world can be more sensitive to the feelings of the younger generation 🙁
曜
日
Oh I didn't take into account the assumption in fine print. Hee... so the probability of the Student having a happy CNY is slightly greater... That should be a small consolation for the Student because at least there are times when these kaypoh aunties can actually remain silent...
曜
日
Yes miracles do happen (when they actually remain silent) but unfortunately no miracle came to Miss Loi's rescue last week 🙁
In any case, happen to stumble upon this cool thingy designed to help future "victims" (especially "older" ones like your truly) pass their time quicker in the coming years:
曜
日
Happy niu year!!
Thanks for the info on the Full month party. I got to be there!!! hehe....