Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths. Her life's calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over 17 years she has been a savior to countless students ... 
that traumatized Miss Loi’s childhood
Ever since a harrowing experience of being pursued by a big bad dog when she was a very cute child, it’s safe to say that there isn’t much love lost between Miss Loi and the canine population.
Unfortunately, being a private tutor means that she often has to live with the occupational hazard of facing big bad dogs at her students’ house.
They range from fierce growling beasts with salivating tongues (which she always gives a wide berth of ≥ 5m) to the cute but irritatingly … umm … hum sup kind who never fail to … umm … climb all over her in an attempt to lick away the top layer of her Shu Uemura makeup, create a saliva trail up and down her legs, and often leaving a helpless Miss Loi thinking …
你虽然得到了我的身体，但你永远得不到我的心！
… as a solitary tear drop flows down her face.
And on this topic, Miss Loi found herself face-to-face with a particularly nasty-looking dog one day, as she waited at the porch for the maid to open the door to her student’s house.
As she stared into its pair of big dark eyes, notice was served of its enormous strength when she found that it was held back by not one but FOUR leashes tied to various points around the porch.
But the maid was taking ages, and a bored Miss Loi decided it was time to exact some measure of revenge for her traumatized childhood.
Yoohoo Doggie … how does it feel to be all tied up huh?
*Sticks out tongue and makes monkey face*
Grrrrr …
Came the friendly reply as it reared its huge white furry head.
Not happy? Come and get me lor. Oops but you can’t! Hur hur hur!
GRRRRRRRRRRR!!!
And so in a severe lesson on complacency, the angry dog managed to break one of the leashes in a mighty show of strength, just as her (petrified) student appeared at the door!
Miss Loi! Three leashes won’t hold him for long! I have a rope I can throw to pull him back by the neck - but I dunno how long I should throw?!
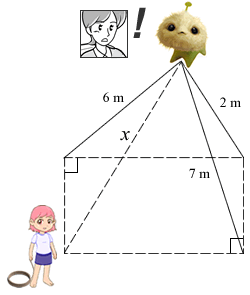
Given that the lengths of the three remaining leashes are 6m, 2m and 7m, and that they are tied to three corners of a rectangular area, with Miss Loi’s student standing at the fourth corner.
Find x, the length of the rope, that the student must throw.
Miss Loi how?! You know I’m only Sec Two! I haven’t learn Trigonometry yet!!!
Now isn’t the time for excuses! Sec Two students should be able to solve this - I’ve just taught you Pythagoras Theorem last week!
Can you please help Miss Loi before she becomes dog food?!
Comments
Comments Feed
10 Comments
曜
日
The answer is x=9 right? Haha. I’ve got the solution, but its in paint.
曜
日
http://base.googlehosted.com/base_media?q=hand-6731010861134777345&size=1
Here is the link.
曜
日
This is one of the easier questions here…
1)Breadth of rectangular area is found by:
=
m
=
Therefore, length of rope needed=
=
= 9m
Whew, pmath is driving me crazy… :/
This working is WRONG (but answer’s miraculously correct)! Please see correct workings in this link in comment #2 above! - Miss Loi
曜
日
Someone: Wah you actually drew your workings using MS Paint?! *touched*
In any case, this (being a Sec 2 question) is an exercise on Pythagoras’ Theorem and simultaneous equations.
So the way to solve this is to form 4 simultaneous equations using each of the leashes as hypotenuses of right-angled triangles (please click on Someone’s link for his well-crafted diagram & workings - don’t worry there’s no virus there!)
Hopefully younger readers can see from this example that simultaneous equations don’t only come in pairs like what you normally see in your textbook. Sometimes situations might require you to form > 2 initial equations based on whatever info that’s given in the question (don’t be lazy!).
曜
日
Clarion: Very, very interesting method you have there - and you’ve gotten the right answer!
It appears you’re implying in your workings that:
But bearing in mind this is a 2-D diagram (not a 3-D pyramid as many students mistakenly assumed), Miss still couldn’t find your right-angled triangles despite a prolonged period of staring at the diagram in a Zen-like state.
Please excuse Miss Loi if she has failed to see something that’s very, very obvious as she’s been pretty tired from all the late-night JB petrol pumping for this couple of days
曜
日
I think Clarion assumed you could use the familiar
for all triangles.
曜
日
Ok then, because I thought both triangles form by the leashes were right angled.
曜
日
Clarion: Wah wrong assumption and you still got the right answer!
Seems like the winds of luck are blowing your way - pity it’s not exam season now!
曜
日
I’d wanted to draw a circle round ‘X’ and write on top “Here it is…”
曜
日
Aiyooooo cockcroach that joke has already been mentioned to death in many maths websites!