After thwarting the Persians with the three Spartans, Miss Loi will be busily lighting up many many joss sticks to ‘celebrate’ this long weekend!
To spice up your holidays, she will leave you with a commonly-asked question starring an enigmatic inverted cone of water that has been sighted many many times …
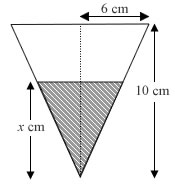The diagram shows a vertical cross-section of an inverted cone of height 10 cm and base radius 6 cm. Water is poured in to a height of x cm.
- Show that the volume, V cm3, of water in the container is (3π/25)x3 cm3.
- Find the approximate increase in V when x increases from 3 to 3.02 cm.
Next time, instead of daydreaming at the water dispensor, why not think about how familiar the little cone you’re drinking from is going to be in your exam? 
がんばって!!!
Subscribe now to the 
Suggested solutions & answers to selected 
my results came out better than expected 
...
Quah Xiao Xi (2)
apocalyptical mecks (1)
confused (1)
Ryan (1)
Serafine (1)
Student_B (1)
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life's calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over 21 years she has been a savior to countless students ... 
9 Comments
曜
日
woah, that was challenging... been like almost 6 years since i last attempted such quesion.
let the unknown radius of the cone with x height be rx
by porportion,
rx = 6x/10
Therefore, by the cone formula
Vx = 1/3π(6x/10)^2*x
= (3π/25)x3
correct?
the 2nd part, Vx3.02-Vx3.00 or
3/25π[(x a)^3 - x^3)
= 3/25π[x^2a xa^2 a^3]
so, let x = 3 and a = 2, and u can solve for the differences.
correct?
hahaha... really been long since i ever did this man!!!
曜
日
Mossie you sure sound like an over-aged student!
Part 1 is correct as you rightly used similar triangles for the proving.
But Part 2 is WRONG! Wrong approach! Wrong formula! WRONG WRONG WRONG!!! *jumps up and down like a siow char bo*
So *tidies hair* I think your 6 years of rustiness is showing
Students, this question is still open - keep trying!
曜
日
hahaha... i can't imagine if my teacher ever jumps up and down, left and right like a siaw char boh...
曜
日
r = 3/5x
v= 1/3 π r^2 h
v= 1/3 π 9x^2/25 x
v= 3πx^3/ 25
v=3π/25)x3 (shown)
dv/dx = 9/
3625π x^2 (thro quotion rule)delta v = dv/dx times 0.2 (with x as 3)
delta v = 0.648 π
correcto?
曜
日
Kiroii, answer correcto but working a little incorrecto which Miss Loi already corrected in red for you. Judging by the time of your answer, think you're a bit sleepy lah.
Mossie see how the model student did it??? You can't just anyhow substitute the x values directly into the above volume formula!
You are finding the change in V (i.e. dV) with respect to a small change in x (i.e. dx) so you die die have to differentiate first!
曜
日
Familiar TYS qn....
曜
日
Now that it's O-Level crunch time, more familiar 'must-do' questions will be coming your way.
Do ask your fellow
sufferersfriends to come here to get an idea of the commonly recurring questions and also burn some joss sticks!曜
日
ok a stupid question. must memorise figure formulas anot ar. like cone. ok probably too late to ask.
曜
日
But of course! How many times have you seen 1/3 πr2h served to you on a platter?