UPDATE: Thanks for guiding Chang-Er Miss Loi safely to the moon. She shares some heavenly mooncakes with the rabbit last night! Yummy!
While the ritz and glitz of last Friday begins to fade into memory, the Mid-Autumn Festival is here again!
A time to commemorate a legend, a time for Hello Kitty lanterns with endlessly-repeating subliminal tunes, and a time when Miss Loi receives some delicious mooncakes from students and friends to gorge herself silly.
And so feeling rather hungry after a long day of lessons, she decided to drive to a nearby park to devour savour those mooncakes under the moonlight, totally forgetting what happened the last time she did some … umm … moonlighting.
In popped a snow-white morsel into her mouth, as she closed her eyes and surrendered to that heavenly flavour creeping up her taste buds, with the full moon looming large and bright above.
Unfortunately, no one told an alcohol-intolerant Miss Loi that the mooncakes were laced with liquor, and she soon found herself feeling tipsy coupled with a floating sensation …
.
.
.
When she opened her eyes, she discovered to her horror that the moon was now very much larger than before, and appeared to be drawing her towards it like a tractor beam!
As her long hair trailed in the cool night breeze, she had an even greater shock when she looked back and realized that she had left her handbag (yes the same big un-glam one she carried upstage last Friday) on the park bench that was rapidly receding into the distance – causing her to struggle like a mad woman in a bid to retrieve her bag.
Alarmed by what she had just witnessed, a rabbit stopped whatever she was pounding on the moon and yelled out to Miss Loi:
OMG you’re the Chang-Er with the WORST buoyancy control I’ve ever seen!
Stop struggling!!! You’re veering off-course! Land on the moon ASAP or you’ll be heading for outer space!
Invoking her powers of Coordinate Geometry, Miss Loi saw that:
The circular moon has a centre that lies on the line:
2x + y – 1 = 0
and its circumference passing through the points A(-2, 0) and B(5, 1).
To help Miss Loi land safely on the moon, find the coordinates of its centre and its radius, and hence deduce the equation of the moon.
With the introduction of Circles into the New A-Maths Syllabus this year, students are now required to know the equation of a circle, which may be expressed in standard form:
Equation of a Circle in Standard Form
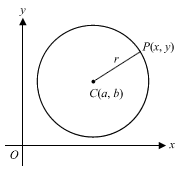
(x – a)2 + (y – b)2 = r2
where C is the centre of the circle at coordinates (a, b) and r is its radius.
N.B. There’s also a General Form (to be discussed at another time)
Also, being a part of the Coordinate Geometry chapter, questions on Circles are often intertwined with bits and pieces from a variety of basic Coordinate Geometry topics like Midpoint of a Line Segment, Equations of Straight Lines, Perpendicular Lines etc. as well as the Geometric Properties of Circles which you’ve learnt in your Sec 3 E-Maths Mensuration.
Hence, good foundation is needed to bring Miss Loi to the moon!
12 Comments
曜
日
Shall attempt this question despite my questionable understanding of this chapter.
*A lonely voice echoes from the moon ...*
Yours is a common approach (found in some textbooks) to first locate the centre of the circle, C(x,y), using the intersection of two lines i.e. 2x+y-1=0 (in which it's given that C lies on) and another line.
So where's this other line?
It always helps to sketch out a diagram right from the start:
From one of the Geometric Properties of Circles you've learnt in your Sec 3 EMaths, you should know that the perpendicular bisector of any chord in a circle will pass through its center.
To find the equation of this perpendicular bisector (i.e. the red dashed line in the diagram above), all you need is to calculate its gradient m and the coordinates of a point (x1, y1)
The coordinates of (x1, y1) can be obtained from the midpoint M of AB, which you've correctly calculated:
1) Midpt. of AB= (
, 
) = (1.5, 0.5)
But what follows here is EXTREMELY TRAGIC: in your basic Coordinate Geometry the gradient of a perpendicular line is
NOT 
i.e. you forgot to invert and you missed out the minus sign!
2) Gradient of AB= (1-0)/(5+2) = 1/7. → CORRECT
3) Gradient of perpendicular bisector of AB:
0.5=1/7(1.5)+c → WRONG!
c=4/14 (eh, weird weird de...) → WRONG!
It's weird weird de because the gradient of the perpendicular bisector should be -7!
y=1/7x+4/14. -- (1) → WRONG!
Remember that one way to express the equation of a straight line is:
So you can just sub the values into the above to obtain the full equation of the perpendicular bisector:
Of course you'll still get the same equation if you had used y = mx + c 😉
4) Centre also lies on 2x+y-1=0. --(2)
solving (1) & (2),
x= 1/3, y=-1/3 → WRONG!
Centre of circle = (1/3, -1/3) → WRONG!
If you had gotten equation (1) correct, you would've obtained the centre of the circle at (2,-3)
Radius of circle2= (1/3+2)2 +(-1/3)2=50/9 → WRONG!
... and the radius to be
Eqn of circle= (x-1/3)2+(x+1/3)2=50/9
=(3x-1)2 + (3x+1)2 = 50/9 → WRONG!
... and the equation of the moon to be (x-2)2 + (y+3)2 = 52
Correct?
NOT correct! It's scary how a little mistake can turn your entire question into a 满江红 doesn't it?
(PS My school mad de lor. Teach differentiation before this topic. DX)
It's late now - shall discuss Li-sa's answer tomorrow *retreats back to the moon*
曜
日
Pretty busy these days. As for the "truncated" comment, I was just trying to do vectors questions before anyone teaches me, but carelessly made a mistake. What .l said was exactly what I thought, and I didn't get into a whirly black hole in space or time.
clarion-x, my school also taught differentiation before circles. It's perfectly fine. We learnt circles just this week.
*A lonely voice echoes from the moon once more*
And a diagram suddenly appears from the sky:
The no-brainer is to Let.
Let the coordinates of the centre be (h,k). Then put (h,k) to 2x+y-1=0:
2h+k-1=0...(1)
How can we find the radius? Think centre, think circumference... aha! The distance between the centre and the circumference is the radius!
Miss Loi loves this approach of yours 😀 - equating two ways of obtaining the radius r to form the second expression for h and k, cutting down a couple of steps as a result!
14h+2k-22=0...(2)
7 × (1) - (2)
7k-7-(2k-22) = 0
7k-7-2k+22 = 0
5k = -15, k = -3
Sub k = -3 into (1)
2h+(-3)-1 = 0
2h = 4, h = 2
.'. Coordinates of the centre = (2,-3)
Radius =
= 5
Equation of the moon:
I must say that this is a little difficult than the textbook's questions, especially the equation (i.e. 2x+y-1=0). But I figured it out by recalling one worked example. It had absolutely nothing to do with linear equations.
It was determining whether a point lies inside, on or outside of the circle. First one must find the radius and the distance between the centre and the point. Then, by comparing the two lengths, the question can be answered.
曜
日
啊，我忘了跟你说：
中秋节快乐！
《水调歌头》苏轼
丙辰中秋，欢饮达旦，大醉，作此篇，兼怀子由。
明月几时有，把酒问青天。不知天上宫阙，今夕是何年。我欲乘风归去，又恐琼楼玉宇，高处不胜寒。起舞弄清影，何似在人间。
转朱阁，低绮户，照无眠。不应有恨，何事长向别时圆。人有悲欢离合，月有阴晴圆缺，此事古难全。但愿人长久，千里共婵娟。
《嫦娥》李商隐
云母屏风烛影深，长河渐落晓星沉。
嫦娥应悔偷灵药，碧海青天夜夜心。
曜
日
But the thing is that we haven't even STARTED on differentiation!
曜
日
And Miss Loi, may you not float off to the moon after enjoying mooncakes again!
曜
日
诗词，只是应节罢了，没什么大不了。
Miss Loi当然不是嫦娥啊！那首《嫦娥》是作者抒情用的，好像人们说「搞什么鬼」不是说真的闹鬼一般。
曜
日
=.= not understand the question at all
going crazy T.T
malaysia education level really so low
曜
日
Bravo Clarion and Li-sa for contributing two different approaches to this problem!
While both approaches are strategically similar in a sense that both seek to find the center coordinates of the circle via forming two simultaneous equations involving x and y (or h and k for that matter), Li-sa's has fewer steps (and a lower chance of careless mistakes) involved by working on the expression for radius r instead of working out the linear equations.
So a great example that textbook answers may not necessary be the greatest and quickest 😀
P.S. Sketching out a quick diagram immediately upon reading the question can often help you visualize the whole thingy and open your eyes to many possibilities 😉
曜
日
And now that
Chang-ErMiss Loi has returned to earth after a delicious mooncake feast ...Clarion: You're from LMBFHSS?!
Li-sa: To complete your profound poem: 昨晚的月餅很好吃喔! 😛
7-inx: Since this is an AMaths question, are you taking AMaths?
曜
日
x.x
I am CMI in Coordinate Geometry the lor.
Any advice before any more tragic mistakes are made?
曜
日
Clarion: 一个英文字 / One word:
P R A C T I C E
*Looks at most recent comments*
Wah suddenly so many homework for Miss Loi to mark! *rubs eyes*
Long hours ahead ...
曜
日
Till the day some robot takes over their marking tasks, teachers' lives remain heroic yet woeful.