After a tumultuous week of near-death experience and some bizarre wrist-slitting, Miss Loi is utterly shocked by the realization that the last A-Maths question was posted almost a month ago on this blog!
So in order to appease the upmarket segment of A-Maths students and LMBFH Syndrome sufferers, here’s one of those irritating composite functions questions that have been appearing repeatedly in the actual O-Level exams (Paper 1 & 2) for the past few years.
The functions f and g are defined by
f(x) = 2√x, x > 0,
g(x) = x − 2, x > 2
Express each of the following in terms of f and g only.
- x → x − 4, x > 2
- x →
 , x > 2
, x > 2 - x →
 , x > 2
, x > 2
Miss Loi always tells her students not to anyhow whack, stay calm and know thy approach before attempting each question.
But there’re always exceptions to the rule. So when you see something like the above, guys ‘n gals, it’s Anyhow Whack Time!
Before you start taking out all your religious artifacts and start chanting in the exam hall, do remember that it’s not all about randomly trying out your fg, gf, f2, g2, f-1, g-1, f-1g, g-1f, f-1f, g-1g …
NOTE:
As the sagely saying goes “Anyhow whack also must whack smartly!“, please look at each final expression in the question:
- If it looks a little similar to f(x) or g(x) then trying whacking fg, gf, f2, g2 first.
- If it looks drastically different from f(x) or g(x) e.g. part 3 of the question above, then there’s a high chance an inverse function f-1 and/or g-1 is involved.
- Don’t forget the possibility of making use of the answer from an earlier part too!
OK with all these in mind, happy whacking guys and gals!

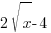 , x > 2
, x > 2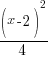 , x > 2
, x > 2

 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















12 Comments
曜
日
erm im rather unsure about my answers but
1) g(x) - 2
2) f(x) - 4
3) [g(x)]^2 / 4
曜
日
kiroii, for these sort of questions you're supposed to express the answers in terms of f and g only (read the question again).
This means your answers should contain no numbers - nothing other than f and/or g.
Has your teacher gone through this topic with you yet?
P.S. You normally start by substituting the expression of one function into another which Miss Loi thinks you're half-way there.
曜
日
i know the first one is gg(x) .. the rest cant solve le ... any other methods to solve this kind of questions other than trial and error?
曜
日
oh got it first is g2 Yup gg(x) = (g(x-2) = (x-2)-2 = x -4
2) is g2(f) Well done! You remembered to use the answer from part 1! i.e. by simply substituting f(x) into g2(x) you'll get 2√x - 4
3) thinking
曜
日
WOOT IM SMART?
for number 3 is
...f-1 g
曜
日
for the 3rd
f-1 -------- y =2 √ x
x2 / 4 = y
with g being x - 2
f-1 g = [(x-2)2] /4
Yes when you see that the final expression looks a bit distant from your original f(x) and g(x), in this case there's a denominator, it's time to consider working out the inverse!
曜
日
Hello STEPH,
There's no hard and fast rule for composite functions questions such as this that involves somewhat working backwards from given expressions.
Actually most of the time the expressions are not that complex (at least in the beginning of the question) and students should be able to 'see' at first glance and substitute in the right functions quickly.
If you're really worried and confused in the exam and need some standard 'steps', as written in this post, go through quickly the sequence of combos like fg, gf, f2, g2 as stated in this blog post. If you still don't get the intended expression work out the inverse and try out the combos of f-1 and g-1.
Also do be alert to the possibility of using any answer(s) from the previous part. E.g. refer to part 2 of this question.
曜
日
WOOT! kiroii is smart! Miss Loi is impressed this time!
曜
日
wa......still reading the solutions... *scratches head*
曜
日
yeah yeah~ eh miss loi im actually rather curious what u look like>.< why not put up ur pic instead eh invite all kinds of surreptitious old fogeys in LOL
曜
日
123: Feel free to ask Miss Loi if you're unclear on anything here.
Kiroii: Thought Miss Loi's pic is all plastered over this website? Else, what kind of pic are you looking for you surreptitious old fogey?! LOL
曜
日
wad de-.- im too much of a gentleman to act clandestinely or lewdly