As D-Day draws nearer, Miss Loi’s Question of the Day gets longer … kekeke.
Besides the arrows and symbols looking exactly the same, there are few differences between E-Maths and A-Maths vector questions. In some schools vectors are even taught exclusively in E-Maths classes, much to the annoyance of the A-Maths student who happens to hate his/her E-Maths teacher!
Take the question below for example. This typical but tedious question is designed to test your elementary vector knowledge like Addition of Vectors, Difference of Two Vectors, Negative Vectors, Scalar Multiple of a Vector, Parallel Vectors, Position Vectors, and always a little bit more. *stops to catch breath*
Wow. That mouthful of words above already constitutes roughly 75% of your A-Maths vectors syllabus!
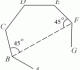
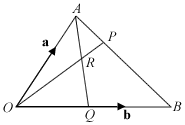 In the diagram,
In the diagram, 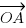 = a and
= a and 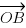 = b. The points P and Q lie on AB and OB respectively so that AP/PB = 1/3 and OQ/QB = 3/4. The lines OP and AQ intersect at the point R.
= b. The points P and Q lie on AB and OB respectively so that AP/PB = 1/3 and OQ/QB = 3/4. The lines OP and AQ intersect at the point R.- Express
 in terms of a and b.
in terms of a and b. - Show that
 (3a + b).
(3a + b). - Given that
 , show that
, show that  = (1 – k)a +
= (1 – k)a +  kb.
kb. - Given also that
 , find the value of h.
, find the value of h. - Find the numerical value of
IMPORTANT: At this stage of the game, it is imperative that students to the scene appreciate the fact that long-ish vector questions have this evil tendency to ask for something a little off-tangent (like ratios and areas – can you spot this in the question?) that will usually require something beyond your vector abilities.
So approach all questions with a pure and open mind and don’t blindly Vector See Vector Do. 不要走火入魔! (literally: don’t keep firing when you’re already misfiring!)
You get the idea.

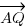 in terms of a and b.
in terms of a and b.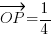 (3a + b).
(3a + b).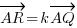 , show that
, show that 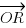 = (1 – k)a +
= (1 – k)a + 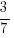 kb.
kb.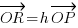 , find the value of h.
, find the value of h.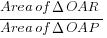
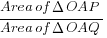
 Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students …
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life’s calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over years she has been a savior to countless students … 





















22 Comments
曜
日
Hey,are you sure it is Emaths?! 🙁
曜
日
Yes it is. O-Level ≠ IB 🙂
曜
日
eh escuse me but is question 3 phrased wrongly? i cant get 3/7kb
1) OQ/OB = 3/4 (See question again!)
OQ = 3/4b
AQ = OQ - OA
= 3/4b - a
2)
 ,
, 
 - 3
- 3 =
=  -
- 
 =
=  shown
shown
3
3)


 + a
+ a
 =
=  b - ka + a
b - ka + a
 a +
a +  kb
kb
3/43/4曜
日
Great effort Kiroii but ... umm ... don't think Miss Loi phrased wrongly.
Please see Miss Loi's markings on your workings 😉
Ready for parts 4 and 5?
P.S. Miss Loi has tidied up your working for readability 🙂
曜
日
oh righto-.- read de question wrongly...anyway can i ask fer some insights as to this question?
A hollow right circular cone is held upside down with its axis vertical and contains 60cm^3 of water. Water is being added at a constant rate of 2cm^s per second and leaks throught the small hole at the vertex at a rate of t/4 cm^3 per second after t seconds.
(i) Find the value of t when the cone contains the maximum volume of water and calculate this volume.
(ii) Given that the volume of water in the cone after t seconds is [pie(h^3)]/ 48 cm^3 where h is the height of the water, calculate the rate of change of the height of the water level when the volume of water is 36 cm^3. Give your answer correct to 3 significant figures.
曜
日
Wow wow wow! This is the first time someone actually 'shoots' a question back to Miss Loi right in the middle of her blog!
Before Miss Loi the Student attempts this question, may she ask Teacher Kiroii a few questions first?
1. Miss Loi assumes your 2cm^s per second actually means 2cm3 per second right?
2. Miss Loi suspects that in order to do part (ii), you require the answer from part (i). So would like to check with you if what you have provided is the whole question, or is there some more parts i.e. (iii), (iv) etc.???
Do let Miss Loi the Student know ok? She will obediently pass up this homework to you tomorrow!
Sorry Teacher Kiroii, now a bit late and Miss Loi needs to wake up early tomorrow. *excuses excuses*
曜
日
ya its de whole q sry abt de unclear typin but cant use com to type de exact figures
曜
日
oh btw tis isnt my homework jus one of de star questions i found in my a maths revision book even my teacher cant do-___-"
曜
日
Teacher kiroii,
Very quickly ...
(i) t=8, max volume = 68 cm3
(ii) -0.303
Correct? 🙂
曜
日
wad de-.- how de heck ya acomplished it >.
曜
日
Workings for part (i):
The effective rate of change of the conical volume V,
Max. volume occurs when (note this is from A-Maths chapter!)
(note this is from A-Maths chapter!)
Hence,
Now to get V, you'll need to integrate the equation (again this is A-Maths!):
Given in the question that when t = 0, V = 60 cm3. So sub in the values into the equation, you'll get:
c = 60 and you'll get the full equation of V:
As obtained earlier, V is max when t = 8, so sub in this value of t into the equation for V:
Max. volume =
= 68 cm3
Get the gist here?
曜
日
Workings for part (ii):
So now you have two equations for V:
So when V = 36 cm3, simply sub in this value to find the corresponding h and t:
Factorizing this quadratic equation,
(t + 8)(t - 24) = 0
You'll get:
t = -8 (NA), 24
∴ t = 24 s
Now the question asked for the rate of change of the h i.e. when the V = 36 cm3.
when the V = 36 cm3.
Hence using the Chain Rule (from your A-Maths Rate of Change chapter):
Now you can easily differentiate from the given equation, while
you can easily differentiate from the given equation, while  you've already obtained from part (i), so:
you've already obtained from part (i), so:
Sub in the values of h and t you obtained earlier for V = 36 cm3:
Using your super-duper scientific calculator to calculate the above, you should be able to get
Wow that was some typing! To reward Miss Loi the student from answering your super-duper cheem question, can Teacher Kiroii do parts 4-5 of the original vector question for her? 😉
P.S. This is basically an A-Maths question being answered in an E-Maths blog entry. To prevent potential confusion to readers, try asking A-Maths questions in one of Miss Loi's A-Maths blog entry ok?
曜
日
(4)

through comparison or comparative
1-k = 3/4h
1 - 3/4h = k (1)
3/7k = 1/4h (2)
 though k isnt needed but i find it to be useful in part 5 so>.>
though k isnt needed but i find it to be useful in part 5 so>.>
sub (1) into (2)
Miss Loi: Congratulations! You've got part (4) done nicely - cleaned up your workings a little for better readability! But why are the workings for part (5) spanning across 2 comments??? ... hmmmm ... let me see ...
area of OAR / area of OAP
let h be AR (both share the same lenth for height)
= (!/2 x OR x h) / (1/2 x OP x h)
after cancelation
= OR/OP
= sub in OR and OP from earlier sections and sub in k as 7/16
= (1a - ka 3/7kb) / ([3a b] / 4)
= (9a 3b)/16 x 4/(3a b)
notice 3a b is basically 1/3 of 9a 3b so after combin and canceling we'll get 3/4
area of OAR / area of OAP =3/4(god this question is tedious there has to be a simpler method)
曜
日
5ii) (area of OAR) / (area of OAP) = 3/4
area of OAP = (4 x area of OAR)/ 3
(OAR = 1/2 x OR x AR)
(area of OAP) / (area of OAQ)
= (4/3 x 1/2 x OR x AR) / (1/2 x OR x AQ)
after canceling
= (4/3 x AR) / (AQ)
(AR = kAQ)
= [4/3(3kb/7 - ak)] / (3b/7 - a)
sub k as 7/16
= (12b - 28a) / 48) x [7 / (3b -7)]
point to note 12b - 28a is 4 times of 3b-7a
hence [(12b - 28a)28] / [(12b - 28a)48]
after cancelin..
28/48 = 7/12
(area of OAP) / (area of OAQ) = 7/12
forbearance is appreciated if i got it wrong-.-
曜
日
oh yea can i say IF I GOT IT RIGHT [BEEEEEEEEEEEEEEP!!!] WOOT IM SMART!~ jajaja
Miss Loi: Now, now ... before you get overly hysterical let's keep this blog a family-oriented place shall we? 😉
曜
日
eh so is my answer correct? do offer a different solution? i feel mind is WAY too long winded it sorrta took like 10-15mins for each part in question 5
曜
日
For part (5), your mass of words just increased Miss Loi's myopia by a few notches!
Yes there is a shorter solution. Consider this diagram:
Do you agree that triangles OAR and OAP share a common height h1?
Similarly triangles OAR and OAQ share a common height h2.
From your usual triangular area formula, the only thing that is different are the bases (lying along OP and AQ respectively), but we can express this using the ratio values h and k obtained in part (4). Hence,
Using the value of obtained in part (4),
obtained in part (4),

Using the value of obtained in part (4),
obtained in part (4),

=
Short enough for you? 😉
Remember what was said in this blog entry about vector questions often asking for something a little bit off-tangent?
Your workings for part 5 demonstrates this point perfectly. You started off well (i.e. you were looking for common heights and all that) but then it all became tedious once you start substituting in the vectors. Imagine this in exam conditions. Many students tend to get sucked so deep into the vector 'pit' (afterall you've been solving for vectors till this point) that they've forgotten that sometimes a different approach is called for.
Hope you've learned something from this today. I know you're excited but please, please refrain from swearing here again!
曜
日
yea sry jus tat i kinda amazed myself after seein the gist of solvin it then i started writin franatically and got devoered in melodramatic emotions
ps:wrote it in 2 parts since after doin q 5 part 1 had to meet an acquaintance so left part 2 for later
曜
日
oh yea 4got to thank ya fer solvin my other a maths q thanks..tt question was truly far-fetched and unruly..LOL btw my teacher comment on the question maker sayin he has no life makin such riddu questions but seriously its damn far fetched
曜
日
hi miss loi, more vector questions please
曜
日
Welcome to Jφss Sticks Charmander! Miss Loi shall try to cover as many topics as she can now that exams are near.
曜
日
wow! what a place for math lover!.. i love doing math...guess it could be awesome place where everybody comes and provides solution... 🙂