As typical Singaporeans, we all love our AIO packages. From wash/cut/treatment/rebond/blow/dry hair salon packages to body scrub/facial/massage/honey milk bath spa packages, they usually offer (in theory) better value over the sum of their parts.
In exams, however, evil AIO packaged questions (i.e. those that test you knowledge of multiple topics in one go) offer students plenty of nail-biting moments and the unique opportunity to experience a panic attack.
As a sadist an esteemed educator, it is perhaps natural that Miss Loi has a mild fetish for a question like this:
N.B. This is E-Maths Paper One so NO CALCULATORS ALLOWED!
A, B and C are the vertices of an equilateral triangle which lie on a circle of radius r cm. Using as much information given in the table below as necessary,
| sin | cos | tan | |
| 60o | 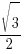 | 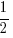 | √3 |
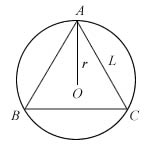
- Show that the length L cm, of a side of ΔABC is r√3 cm
- By comparing the area of ΔABC and the circle, or otherwise, show that 3√3 < 4π.
- List all even integers in the range of 3√3 to 4π.
There you have it.
Something to send you scurrying up and down the chapters of that imaginary textbook in your overworked mind.
Rejuvenated by her facial package yesterday, Miss Loi shall be nice this time and hint that for this particular one, you should bookmark the chapters on Trigonometry, Rational/Irrational Numbers and Mensuration (for once, let’s not joke about this chapter title ok?).
In addition, you’ll need in abundance material from another chapter not found in your book called Common Sense.
But frankly, once you know what you’re supposed to do, this question is actually pretty easy. Hence no formula listed here this time to spoil the fun!
15 Comments
曜
日
Yay, my pleasure to be the first to ans it...
1. Angle AOC is 360° divide by 3 ,which is 120° ........Next, Since cos 60° is 0.5, cos 120° will be -0.5. Then, Using cosine rule....L = √( r2 + r2 - (2r2 cos 120°), Which u will get
√3r2, which isr√3!2.Still think :p
曜
日
Yay, my pleasure to solve the quesion first =)
1.Since cos 60° is 0.5, So cos 120° will be -0.5......By considering Tri. AOC, ( Angle AOC is 120 deg), And then by Cosine Rule...bla bla bla u get r√3!
曜
日
123`, yup cosine rule it is!
Part 1 is the easy one - pure knowledge & memory work. Parts 2 and 3 require knowledge of the chapter not found in your textbook 🙂
P.S. The spam filter is currently marking comments containing mathematical workings as spam. So do not be alarmed if your solution didn't get through. Miss Loi will 'despam' you once she's online, unless you're a Nigerian banker or a pharmacist 🙂
曜
日
well personally since mr 123 here used the cos rule i decided to be saucy by using another method...
let the mid point of BC which is L/2 be h.
by drawing another radius line to connect to B and another line from O to h we'll get an additional triangle.Now
OBH = 30
sin 30 = 1/2 (trigeometry chart)
sin 30= OH/r
1/2 = OH/r
r/2 = OH
sin 60 = (r+ r/2) / L
(root 3)/ 2 = (3r/2) / L
L(root 3) = 3r (after multiplying)
L = 3r/(root 3)
l = r(root 3) after rationalizing ( a maths)
Miss Loi: Well the question says "Using as much information given in the table below as necessary" but you chose to lookup your trigo charts instead. But can't really fault you as your workings showed that you've arrived at the same answer too. Whatever's comfortable for you then.
曜
日
for question two i seek to refute miss loi's statement of the solution being in the book.
area of circle > area of triangle (common sense - Miss Loi: Yes! You'd be surprised many students fail to realize this under exam pressure!)
π x r2> 1/2 x sin 60 x L2
after subing r(√3) = L
and after simplifying
4π > 3(√3) tsk~
Miss Loi: No you didn't refute Miss Loi's statement at all. In fact if you've read the comments properly, Miss Loi would like to thank you for highlighting the name of the chapter that is NOT in the book 🙂
曜
日
and the last question is simply a give away haha? miss loi i bet ur thinking *hah!~ no1 would be as smart as me as to think of how to do this*
anyway
(root 3) x 3 is basically 3.(something)
4x π is basically 12.(something)
to even integers would be 4, 6, 8, 10
Miss Loi: Are you SURE √3 x 3 approximates 3???!!! The nearest higher square root that results in an integer is √4. So your lowest even integer for the range is √4 x 3 = 6. You've rightly approximated π ~ 3, which means the highest even integer for the range is 4 x 3 = 12. But you didn't include this in your answer!
So much for giveaways eh? 😉
曜
日
well frankly i do believe laurels should go to me eh? =x btw the puberscent geometry q i still dont see the gist off it-.- or rather no point staring at the screen
Miss Loi: Answered this at this comment in the original post. Please try to post your comment at the relevant post next time.
曜
日
sorry, didnt mean to spam, coz my comp got crazy, and i accidentally posted twice
曜
日
nah miss loi is nice she wont mind if u spam unintentionally ( unlike what im doin now lololololol)
曜
日
Thanks for trying out the problem!
Please see Miss Loi's comments to some of the workings in red.
曜
日
3√3 to 4π.
eh but if im wrong then how do u calculate 3√3 ?
or juz simply guess?
曜
日
Read the red portion of comment #6 again. The question asks for the nearest integer upwards from 3√3.
Now √3 is never an integer. So is √3.1, √3.2 etc. So the nearest integer is √4 = 2 i.e. the nearest perfect square is 4
⇒ nearest integer from 3√3 is 3√4 = 6 (which happens to be even as well).
曜
日
This is a 没事找事做 comment:
We are looking for even integers greater than 3√3 right?
Assuming we have no clue the approximate value of √3 (and apparently cannot use calculator for this), your comment #12 only mentioned 3√3 < 3√4 = 6 therefore '6' is part of the answer.
It didn't address the problem of what if 3√3 < 4? Then '4' would be an acceptable answer le.
Perhaps you can convince me that common sense says √3 > 4/3 therefore 3√3 > 4?
曜
日
Oh dear no one told Miss Loi there's an external audit of the old blog posts today?!
Alright Miss Loi's original approach was to go for the nearest perfect square which is 4
⇒ √3 > √4
⇒ 3√3 > 3√4
⇒ 3√3 > 3(2) = 6
BUT thanks to your question, Miss Loi now thinks that a more robust approach instead would be to square the original term and find the nearest perfect square that's greater than this squared-term i.e.
⇒ nearest perfect square (that's smaller than 27) = 25 = 52
⇒ (3√3)2 > 52
⇒ 3√3 > 5 (∵3√3 & 5 are both > 1!)
⇒ next integer is 6 (since 62 = 36 > 27)
With the second approach, we not only confirm that 3√3 is confirm chop stamp greater than 4 (with no common sense used, no cheating by calculator), we can also solve the question even if it's changed to List all integers in the range of 3√2 to 4π. (Note: the word 'even' is taken out)
Great
auditquestion from you mathlover - it's stuff like this that fine-tunes the solutions posted here and keepsMiss Loi on her toesMiss Loi's mind well-oiled. If only there are more such though-provoking questions like this in class instead of "Miss Loi! I dunno how to do!!!" *complete with pouted lips* ... sigh ...Ah ... the power of social media ...
曜
日
Ah much clearer now, and it makes use of properties of square root and inequalities too. It is looking more AIO than before.
Great answer from you Miss Loi - it's stuff like this that keeps students
like meinterested to probe further into the wonderful world of mathematics. If only there are more such light-at-the-end-of-the-tunnel answers in school instead of 'this is not in syllabus, no need to know', or 'know one method is enough, wait u confused'.. sigh.. 🙁Since Miss Loi is so nice to answer a 没事找事做 question, I will answer your question too.
I am
an auditor of maths questionssome nightmare maths student who loves asking teachers this kind of questions.P.S. I haven't finish
scrutinizingreading your older blog posts.