On a day when Singaporeans were admiring the modern contemporary design and user-friendliness of a certain toilet, Miss Loi was shopping for her new collection of clothes at a boutique in Orchard Road – something she had planned to do all along over a period of time.
As fate has it, a confluence of factors made it possible for Miss Loi to shop this day, namely: 1) The new collection has just arrived, 2) There’s a store-wide sale going on, and 3) her tuition session has just been postponed.
A sexy set of yellow top and a pair of green bottoms caught her fancy, and she proceeded to try them out in the smallish fitting room, after being accompanied there by the store’s Ah Lian sales assistant.
After locking the fitting room door and flipping her set of clothes over it, Miss Loi suddenly detected a faint burning smell coming from beyond the room.
Sensing danger, she desperately tried to unlock the door but as fate would have it again, another confluence of factors contrived to land her in trouble, namely: 1) A fire had started in the boutique, 2) the door lock was stuck, and 3) she neither had the space nor strength to kick the door open.
To make matters worse, she got the following reply when she shouted to the Ah Lian sales assistant for help:
Sorry I need to call my boss first to see if she allows me to kick open the door! Wait the door damaged and she cut my pay how?!
Just when all hope seemed lost, she looked up and spotted a stylish un-grilled window on the wall! Using her powers of mathematical geometric projection …
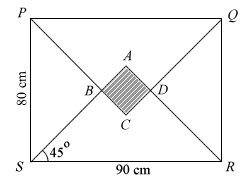
PQRS is a rectangle. The window ABCD is a square. M is the mid-point of PS.
- Prove that ΔPBS ≡ QDR and state the case of congruency.
- Calculate the length of BM and hence, calculate AC.
- Find the area of the square ABCD.
Given that a vain Miss Loi has always known herself intimately (mathematically speaking) and that the largest cross-sectional area of her *ahem* lithe figure is only 30 cm2, should she attempt to escape through this window, or wait for the Ah Lian to get permission from her boss?
A quick decision is needed, for there are only 11 more minutes before the fire overcomes the boutique!
IMPORTANT: To add to the congested confluence of factors, in a fit of panic, Miss Loi has suddenly forgotten all her trigonometry formulae!
But fortunately this can be done by simple calculation using Similarities & Congruencies concepts learnt in Secondary Two, where students are typically not taught the likes of Trigonometry and Pythagoras’ Theorem yet.
So in a desperate bid to solve this, Miss Loi has to recall these hieroglyphs:
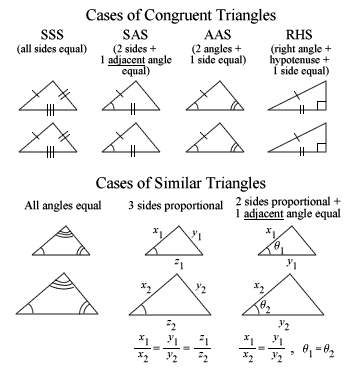
*Please, please remember that for all cases involving two sides, the angle has to be adjacent (i.e. in-between the two sides concerned)!
Lastly, note the word hence appearing in the question, and recognize that, unlike some toilets, not all diagrams are user-friendly enough to include all information from the question (e.g. the whereabouts of point M) → write down all unrepresented info in the diagram as soon as you see them in the question to prevent yourself from getting confused later (especially in your upcoming Mids).
36 Comments
曜
日
Wow...real cool to draw up trigo fomula. By the way, is there any mathematical formula to relate Mass, Height, Impact and the Degree of Severity base on my post at: http://blogofsorts.wordpress.com/2008/04/22/where-did-the-toilet-paper-come-from/
曜
日
Miss Loi, you must be the most un-complacent person in Singapore! But Miss Loi, I must ask you, do you have 7 rolls of toilet paper to break your fall when you escape via the un-grilled window?
曜
日
*stares blankly at all the math and graphs*
曜
日
Ordinary Guy: Got trigo formula meh?
Handsome Soupie: This is a fitting room NOT a toilet - got toilet paper meh?
Krisandro: Got graphs meh?
ALL OF YOU NEVER READ THE QUESTION PROPERLY! MINUS MARKS!!!
曜
日
soup - MissLoi isn't as heavy as the "other guy". She only needs THREE toilet rolls ok? Well since this is a fitting room, then in that case, make that three dresses hahaah!
smc - wow....only 30cm squared huh? *drool*....
曜
日
Hey,the male urinal got door, I won't be surprised that the dressing room got toilet bowl! Haha.. Maybe Miss Loi can tie up all the dresses and abseil down! 😛
曜
日
FoxTwo + Soupie: Why are you discussing what might happen outside the window when it has not yet been proven if Miss Loi can actually squeeze through the window without getting stuck in the process (and getting her legs roasted into little sexy chicken drumsticks)?!
曜
日
alamak u juz make me hv nightmares again. heng i already pass out from e edu system. 😀 students these days so lucky gt tutor like u.
曜
日
Yellow on green on bottom????( He! He! I am trying to image how u look! )
According to common sense if u cannot or unsure if you can squeeze throught the small hole then u can always take off whatever u r wearing & then I am very sure u can go through the hole. It is much easier for a nakel body to squeeze thoudht a hole then a fully clothed fellow!
This is what u should do! Afterall ur life is more important then ur modestry!
Beside this is there is no time for u to caculate if the hole is big enought for u to squeeze thought! The fire is burning! Take off all ur cloths quickly before u burn ur hair!!!
See! So do I get 100% for this question!
曜
日
|c3^sNoW: Thanks & Welcome to Jφss Sticks! You'll never know when such maths knowledge might help you in situations one day *touch wood!*
HAM: Singapore has no winter - so the thickness of the clothes do not contribute to the confluence of factors at play.
You wish Miss Loi to get her tender skin bruised is it?! So 黑心!!!
曜
日
ryn: oohh do drop me a note when u do come! ^^
n er, i hope i only do get to use things like, statistics and algebra and never ever 3D trigo =X most nightmarish topic ever.
曜
日
|c3^sNoW-chan: You're spared from your nightmare here, for this is not a trigo question 😉
曜
日
tsk tsk.. there's a fire raging outside and you're worried about BRUISING?!
*shakes head*
曜
日
Haha Miss Loi's sexy body can't afford any bruise..Haha..don't worry Miss Loi, the ministar will save you.
曜
日
狐狸二号: 如过为了逃过这场灾难，而应此被留下终生的疤痕，那我宁愿不要活了！
Soupie: Only if the 'ministar' knows how to solve Similarity & Congruency math problems - which should be peanuts for them, else they wouldn't be 'ministars' right? 😉
曜
日
er, mini-star dunno how to solve la. only BIG star will noe. 😀 *runs n hide b4 ministars' minions come catch me*
曜
日
Hi Miss Loi,
You may have heard about the latest most view videoclip described in STOMP relating to "Ghost in Raffles Place lift. Real or Fake? The STOMPer also has blogged about his experience at his blogsite SG Office Ghosts. Any maths equation to determine if the apparition is real or fake? Or perhaps any protective cure from the Temple in case some of us might encounter such a situation? Pls enlighten.
P/S : Perhaps you may like to place this comment as a new post.
曜
日
|c3^sNoW: Wow ... the extreme lame nature of your statement can be tantamount to committing a 'grave offence' - punishable by reading this blog from front to back 100 times under the Penal Code!
Ordinary Guy: *shuts down computer, turns off monitor, jumps into bed, pulls blanket over head and trembles in fear* GOOD NIGHT EVERYONE!!!
曜
日
wahaha i dun mind such punishment..since u nv say..solve e problems :p
ryn: u lor miss loi. who else. thanx!! 😀
曜
日
Miss Loi, you should say this now: "No answer? Now I guess that settles it". Since here got no answer at all.
曜
日
Ignorantsoup: Guess that settles it when Miss Loi becomes a roasted chick 🙁
While Miss Loi is still deciding on whether it's worth bruising herself in order to escape, Sergeant Loi has been placed temporary in-charge of this place for now.
曜
日
1)
i) Since PQRS is a rectangle, opposite sides have equal lengths. I.e
PS=QR=80cm
ii)Angle ADC= Angle ABC= 90˚ (ABCD is a square)
By “vertically opposite angles”,
Angle PBS=Angle QDR=90˚.
iii)Angle ASR= Angle ARS= 45˚ (angle sum of triangle)
Angle QRD= Angle PSB= 45˚ (complementary angles)
Hence both triangles are congruent because 2 angles and 1 side are equal, case of congruency is AAS.
2) & 3) still solving 🙂
曜
日
Oh finally someone to
roasted chickMiss Loi's rescue!Miss Loi has inserted a diagram here for greater clarity:
⇒ ∠ABC = ∠ADC = 90o
⇒ ∠PBS = ∠QDR = 90o (via opposite angles)
⇒ equal angle
⇒ ∠PSB = ∠QPD = 45o ⇒ equal angle
So you have 2 equal angles + 1 equal sides and you have the AAS case of congruency (as shown on the chart above).
Well done and 3 marks (one for each prove) to you if you do this in your exam!
Now that you've already proven that ∠PBS = 90o and ∠PSB = 45o which
⇒ ∠SPB = 45o
Can you perform a bit of isosceles magic + similarity ratios for Part 2? 😉
曜
日
I have never come accross a fitting room with a window in all my years of shopping. The example who prove more realistic should Miss Loi choose to say that she was actually using the toilet in a shopping centre, and the toilet cleaner needed permission from the building manager to kick the door down.
曜
日
Ah someone is taking this too seriously..hahaha
曜
日
Welcome to Jφss Sticks ... umm ... MLNE
where windows suddenly appear on fitting room walls😀Soupie: Why are you laughing? What's so funny? Be serious!
曜
日
wah! isn't part a similar to last year's GCE 'O' question?! hahaha!
曜
日
Hello pooboi! How come nobody informed Miss Loi that she made a guest appearance in last year's O Level paper?!
In any case, the first part of congruency questions normally requires you to prove (if it carries > 2 marks), or simply identify/state the congruent triangles (if it carries 1-2 marks).
Speaking of which, parts 2-3 of this question are still unsolved. Clarion you do homework do halfway!!! Tsk tsk.
曜
日
Paiseh lah... No time...
XD
曜
日
Miss Loi won't reveal answer if we don't attempt so..
* A chao tar Miss Loi rises from the ashes ... to present the following diagram: *
2.Last hint given, angle SPB = 45°
Angle PMB = 90° (?)
So angle PBM = 180 - 45 - 90 = 45°
(sum of angles in triangle),
so we've isosceles triangle PBM
Since M is midpoint of PS, PM = MS = 80/2 = 40cm
By isosceles triangle, BM = PM = 40cm
Yes, when answering longish multi-part similarity & congruency question like this one, it's always a good idea to use whatever proofs you've already established in earlier parts.
So from Part 1, we have:
∠ABC = 90° & ∠PSB = 45°
⇒ ∠SPB = 45° (sum of angles of ΔPSB)
⇒ ΔPSB is isosceles (∠SPB = ∠PSB = 45°)
Since ΔPSB is isosceles and given M is mid-point of PS
⇒ BM bisects ∠PBS ⇒ ∠PBM = 90°/2 = 45°
⇒ ΔPBM is also isosceles (∠MPB = ∠PBM = 45°)
⇒ PM = BM = 40 cm
*Extend PC to RS & let intersection point be T.
Angle PTS = 45°(corresponding angles,BM//TS?)
Triangle PTS is isosceles since angle SPT=PTS
so TS = PS = 80cm
RT = RS - TS = 90 - 80 = 10cm
DB = RT = 10cm (?)
so AC = 10cm as diagonals of square are equal
in length.*
* * is crap. Also didn't use BM at all in working.XD
* Deng Deng Deng Deng ... *
When the magic word Hence is uttered in a Hence Question, thou MUST follow the Holy Word and refrain from resorting to your pagan methods, even though your final answer is correct!
So in order to use BM to find AC, you'll first have to proof that ΔPBS and ΔABC are similar:
We already know that ∠PBS = ∠ABC = 90°
Since ABCD is a square,
⇒ AC bisects ∠BAD & ∠BCD
⇒ ∠BAD = ∠BCD = 90°/2 = 45°
⇒ ∠BAC = ∠PSB & ∠BCA = ∠SPB (all angles equal! - highlighted in red in diagram)
⇒ ΔPBS and ΔABC are similar (AAA)
Armed with this revelation, we have the following ratios:
(where X is the midpoint of AC)
And since we've also proven in Part 1 that ΔPBS ≡ ΔQDR, and given once again that ABCD is a square, can you see from the diagram that BX = 5cm?
So ...
⇒ AC = 10cm 😉
3.Area of square ABCD = 2 x (½ x 10 x 5) = 50cm2
(Reason:diagonals of square bisect each other at
right angles.)
For Part 3, there's no holy Hence word to command what approach you should take, so your answer is fine 🙂
Just to highlight another approach should you be required to use AC from Part 2:
Since ABCD is a square, let AB = BC = x
Using Pythagoras' Theorem,
AB2 + BC2 = AC2
⇒ x2 + x2 = 102 (using value of AC obtained in Part 2)
⇒ 2x2 = 100
⇒ Area of ABCD = x2 = 50 cm2 😉
Awaiting enlightenment...
曜
日
Thanks Miss Loi for thy clarification. I've just learnt something obvious which may not be explicitly stated in textbooks.
From your working for 2nd part of part 2 ie. finding length of AC, notice that ratio of corresponding heights (BX & BM) of similar triangles is same as ratio of corresponding sides (AC & SP). This knowledge can be applied when solving questions involving heights of similar triangles.
曜
日
Kiddo: To be honest, as a chao tar Miss Loi was squeezing her *ahem* 30 cm2 figure through the 50 cm2 window, she was sort of expecting some students to protest:
For this, Miss Loi's answer would then be:
曜
日
For part 3, can we use this approach?
Since from part 1 we proved ΔPBS ≡ QDR, and given that ABCD is a square, and both points B and D are common, doesn't that imply that the line AC is the line of symmetry of that diagram?
Hence by letting X be the centre of the square ABCD, we can conclude that BX = (90/2)cm - 40cm = 5cm.
Without go through another round of proving similarity...
曜
日
Almost a year has passed, and the thick smoke that had previously obscured her vision has finally cleared to reveal a chao tar Miss Loi emerging from the ruins of the fitting room.
She rubbed her eyes at mathslover's express method and lamented, at the same time, the tunnel-vision nature of her original 'safe' approach where she, like many stressed students in an exam, ended up having to prove that ΔABC & ΔPBS are similar first.
But if only she had stopped, taken a deep breath and a step backwards, she would've seen mathslover's line of symmetry slicing through the diagram, and used this to quickly obtain AC even earlier in Part 2 as follows:
⇒ DM' ⊥ QR & M' is mid-point of QR
⇒ MBDM' is a straight line (your line of symmetry) (=90 cm)
⇒ BD = 90 − 2(40) cm = 10 cm
Since AC & BD are diagonals of square ABCD, AC = BD = 10 cm
And since the diagonals AC & BD divide the square into four right-angled triangles with height = base = 10/2 = 5 cm, we can simply get the area via 4 × (1/2)(5)(5) = 50 cm2
It must have been the smoke she breathed in ... but
WHY DID IT TAKE ONE YEAR FOR SOMEONE TO RAISE THIS?!
曜
日
lol... turns out someone wanna see u chao da XD
曜
日
@qwerty1106: Some of the readers here are a bit 黑心 (chao tar heart) one you dunno meh?