(N.B. pepper soup they are NOT)
Let’s spin a globe
Find a place to go
Travel the world
We’ll take it slow
We’ll be as one
Everywhere we go
Under the stars
Our hearts will grow
As we move on impulse~!!
Heeding the imploring appeal from a track on Ah Lian DJ Loi’s playlist, Miss Loi decided on a ‘quickie’ getaway last week, to give herself a break after five months of non-stop joss sticks sessions, before the June holidays come to hammer present her with yet more grueling joss sticks sessions till the end of the year.
The ‘spin’ of the globe this time, however, brought her only as far as the neighbouring country to the north, and after stopping for a meal of bak kut teh at its spiritual home, she soon arrived at her final destination.
A place by the sea …
A retreat for her senses …
A place where she would find relaxation and escape from maddening students crowds …
And thus after dumping her luggage in her room, she wasted no time in heading straight for the spa beside her chalet to treat herself to a bit of holistic goodness and rejuvenate her body, mind and soul.
Opting for an 1-hour session of their signature massage using their top-of-the-line aromatherapy signature oil, she soon found herself lying prone on a soft, narrow bed high above the sea.
Before long, top-of-the-line signature essential oil was being applied on her bare back, gently flowing across her body in harmony with the soothing piped-in spa music, a teasing precursor of what was to come.
so this ‘blissful’ image will have to do
And then she was in spa heaven.
A chorus of gratitudes greeted her from every sore muscle in her svelte frame, as the masseur skillfully kneaded away the tight knots from back to front and head to toe.
For an hour, she was truly at one with her innermost senses. The worldly rigours of joss sticks sessions seemed so far away, and all that seemed to matter was the gentle strokes of the masseur and the sound of the waves slapping the stilts below. In fact, so tranquil was the experience that she even forgot (albeit temporarily) how to factorize quadratic equations and solve simultaneous equations with two unknowns.
Finished, Mdm.
It was over, all too soon.
Oh how she yearned for it to last just a little bit longer, to enjoy the feeling of being pampered once more – a sensation that would surely be but a distant fantasy when she returned to pamper coach her students at The Temple … and so …
Ooh your massage was heavenly! May I extend for another hour?
Thank you Mdm. Let me check with counter first. One moment please …
*dials phone*
[Translated from Bahasa Melayu]
Counter … counter … Room #123 wants to extend 1 hour. Boleh?
Nona, a Datuk is coming for massage later and our signature oil is running low.
You may extend your session but make sure you have at least 2 cm depth of oil left in your jar at the end of your session, because Datuk is XXXL size!
With that, the masseur Nona informed the eternally-grateful Miss Loi that her session had been extended, and proceeded to pour more oil on her back, carefully leaving just about 4 cm depth of oil in her conical jar ‘just to be safe’.
When Nona was finished with pouring the oil and placed the jar upright on the table, a sudden horrifying realization dawned upon her and she frantically dialed the phone again.
Counter! Counter! Your 2 cm depth of oil is measured from the tip or base of the jar?!
Alamak! Of course from the base lah! You goondu or what?!
Diagram I
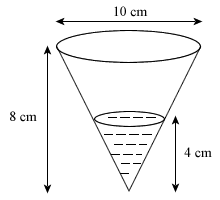
The conical jar has a diameter of 10 cm and a height of 8 cm and is currently left with a depth of 4 cm of oil when inverted, as shown in Diagram I.
-
- Find the volume of oil in the jar, in terms of π.
- Find the surface area of the jar that is in contact with the oil.
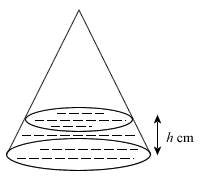
- When the jar is placed upright (see Diagram II), calculate the depth h of the oil in the jar.
Diagram II
Hence let Nona know if this is going to be her last massage at the spa.
The completion of the 
Subscribe to 
Suggested solutions & answers to selected 
kanza (1)
Miss Loi is a full-time private tutor in Singapore specializing in O-Level Maths tuition. Her life's calling is to eradicate the terrifying LMBFH Syndrome off the face of this planet. For over 22 years she has been a savior to countless students ... 
15 Comments
曜
日
ai) by similar triangles,
aii) let slant height be x.
( 3 s.f)
by pythagoras theorem,
=
surface area=
=
Part B: figuring out
曜
日
a) By similar triangles,
diameter of oil = 5 cm
radius of oil = 2.5 cm
ai) volume of oil =
By Pythagoras theorem,
(3 s.f.)
slant height of oil =
aii) Surface area of jar in contact with oil =
b) Volume of container =
Volume of empty space when container is turned upside down =
Considering the similarity of the empty space and the container,
height of empty space = cube root of 445.44 = 7.64 (3 s.f.)
Hence, to Nona's horror, the height of the massage oil left is only (8 - 7.64) = 0.36 cm! Oh dear!
曜
日
careless -.-
曜
日
@clarion-x: Indeed, sigh... everytime I answer Miss Loi's questions here I make stupid careless mistakes... =.=
Volume of container should be
.
And hence after substituting all the right values later on, .. ...
we get height of
oilempty space = 7.65 (3 s.f)(Miss Loi: Is there some rogue joss stick aromatherapy smoke that somehow induces carelessness on this website???)
Not much difference after all, Nona's still in big trouble... :X
曜
日
@mathslover: @ Miss Loi: No, I don't think my monitor is capable of transmitting any rogue joss stick aromatherapy smoke that you send over the cable.
I swear its the green background 在作祟。
It reminds me of the World Cup.
曜
日
For the first time in many massages, Nona's technique was uncertain.
Gone were the slow and steady, rhythmic strokes that sent Miss Loi to a deep slumber in the past hour. In fact they now resembled the noob stuff one gets from a $16/40 min 'promotion' at People's Park Complex
For despite the blatantly low level of oil left in the jar, Nona, like a stubborn student who persistently hides from reality and is not being honest with him/her academic situation, refused to believe it to be <2 cm.
As if on cue, a breeze suddenly blew in from the sea, flipping the pages of Miss Loi's exam papers lying on a side table till they settled on the Mensuration and Similarity topics.
They revealed to Nona that the volume of a cone Vcone is often given in the formula sheet as
and that, for some reason, cones in mensuration questions often involve playing around with the ratios of the height/volume/areas of similar figures.
And suddenly, through similar triangles, she was able to obtain the radius roil of the inverted cone of oil in Part (a)(i) as
roil =
= 2.5 cm
Acknowledging that her math foundation is not strong, she carefully drew out the similar triangles (see diagram above) so as to avoid typical careless mistakes like the one below:
The joy of solving her first ever mensuration problem was indescribable as she excitedly sub in roil = 2.5 cm and height h = 4 cm into the cone volume formula in (1) to obtain
Voil =
cm3
*Of course you may use the bigger similar triangles in mathslover's method but then you'll have to remember to divide the obtained diameter by two to get the final radius, and ensure you don't somehow use the wrong value in later parts which may result in kua kua kua careless mistake like the one committed by clarion above *kua kua kua*
The pages flipped again and revealed to Nona that the curved surface area of a cone is also given in the formula sheet as
The only thing that's missing here is the slant height l, and Nona applied with glee the Pythagoras Theorem she learnt in Sec One at her village school that allowed her to quickly obtain:
l = √(42 + 2.52) = 4.717 cm
And sub in l = 4.717 cm into (2), she happily obtained the answer to Part (a)(ii):
Surface area of jar in contact with oil
= π × 2.5 cm × 4.717 cm
= 37.047 cm2
≈ 37.0 cm2 (3 sig. fig.)
...
曜
日
Just as she was about to give up on Part (b), the breeze blew and the pages flipped again, settling on the topic of volumes of similar figures, with the following expression glaring at her:
Suddenly she realized that despite the dimensions of the water and empty space having changed when the jar was flipped upright, their volumes remained the same.
At this point mathslover's approach of calculating and using the absolute volumes of the empty space & cone is safe and sound provided they can be calculated (which in this question they are).
Miss Loi shall provide an alternative approach just in case you meet a similar question that is evil enough not to provide any means of obtaining the absolute volumes (or areas for that matter):
When the jar is inverted,
⇒ Vcontainer = 8 × Vwater
⇒ Vempty space = Vcontainer − Vwater
= (8 × Vwater) − (1 × Vwater)
= 7 × Vwater
When the jar is upright,
And now for Nona's moment of truth *teng teng teng teng*
∴ h = 0.3483 ≈ 0.348 cm (3 sig. fig.)
...
曜
日
Hi Miss Loi,
I've been to your blog before, but left no comment under my name. And now I've found your blog mentioned here, and the article that accompanies it is a rather interesting read.
曜
日
Actually, considering Nona is able to touch the physical bottle of oil, all she needs is a trusty old ruler... ...
曜
日
@mathslover: Actually she didn't even need a ruler.
Any naked eye would be able to tell that ~3.5 mm was way below the requisite 2 cm of oil.
In any case ... you know ... now that Miss Loi is back in Singapore, she can report that the massage was absolutely lifeless at the beginning of the extended period.
So annoyed was she that she was about to make a complaint when the phone rang again to inform the masseur something about some big-shot canceling his spa appointment ...
... and then all was well again
曜
日
算了。Just delete my previous comment and this one.
曜
日
@Abigail: ??? That Squidoo page got hijacked?
曜
日
@Miss Loi: No. I deleted it later after some consideration.
曜
日
While I gazed at the words "Let's spin a globe", I came across a website that might intrigue you when it comes to a very basic question every science and mathematics student faces: does the earth move? (You can click on my name for details.)
曜
日
The best way to enhance your ability on dealing math equation. Much appreciated to have that kind of massage. Multi tasking purpose to maintain the capability of brain development. And constant practice makes perfect.
From Lindy's blog: how to get rid of stretch marks
One Reaction
曜
日
Intimate photos from my Port Dickson retreat last week, with an intimate account of an incident at the spa: http://bit.ly/bhDoJQ