The howling started at 11pm on Wednesday night, filling The Temple with an air of fear that was quickly followed by eerie rattling sounds coming from the roof above, as if its tiles were being systematically peeled away by whatever’s behind these ungodly noises.
With thoughts of being in a scene of a Korean horror flick (where the actress usually dies) flooding her mind, Miss Loi decided to abandon the Kinematics question she was doing and quickly closed shop for the night.
The curls of her hair were instantly straightened by a mighty gust of wind the moment she stepped outside the Temple Gates, to be greeted by an extraordinary scene unlike any she had ever witnessed: leaves, twigs, plastic bags and whatever <1 kg were strewn everywhere as gale-forced winds lashed through Novena.
Closing her agape mouth just in time to prevent any unwanted debris for supper, Miss Loi recovered her composure and tried to make a dash for her car under the deafening roar of the wind.
Oh it was not a pretty sight as her hair parting constantly changed directions as the wild tempest battered her from all directions – with flying twigs that threatened to scar her precious face, and NTUC plastic bags & the odd flying underwear that threatened to smother her at every turn – all while being mocked by Ivy Lee in brochures blown from the neighbourhood slimming centre.
When she finally hit the road on her way home (albeit with a new hairstyle), she found to her dismay the roads perilously littered with leaves and branches, with huge fallen trees blocking her way 🙁
Miss Loi’s car first passed a big tree located along the way at a fixed point O at a speed of 210 m/min.
Assuming that she moved in a straight line and that her acceleration a m/s2 at t minutes after passing O is given by a = 60t − 240,
- Calculate her speed at the second minute.
- Given that she had to turn back immediately to the direction she came from upon encountering a fallen tree, find the value(s) of t when she had to turn back.
- If the big tree at O was felled by the wind at the tenth minute, will she be able to pass it before it fell? Calculate the total distance she would have travelled in 10 minutes.
To further what’s being taught in its EMaths counterpart, AMaths Kinematics introduces the terms displacement (s) and velocity (v) which may be very loosely considered as distance and speed involving direction respectively.
So instead of that headstrong cyclist/car/train in your E-Maths Kinematics who somehow lost its reverse gear and end up moving in only one direction, you’ll find in AMaths modern cars like Miss Loi’s (or more commonly ‘particles’) that can move back and forth like a maniac in opposite directions, with the following relationships between displacement (s), velocity (v) and acceleration (a):
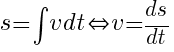
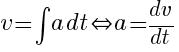
P.S. Most of the above story is true, except the part on the flying underwear. Maybe Mother Nature was trying to tell us something on Earth Day 2009?
10 Comments
曜
日
Why are you driving so slow past the big tree anyway? 12km/h, people run also faster hehehehe!
曜
日
Safety first! The roads were strewn with debris!
曜
日
To prevent hair from such incidents again. I suggest shaving it all off.
"Diary of a BOTAK Private O Level Maths Tutor"
Cool huh?
曜
日
u speeding at 0.12km?
(^_^)
曜
日
Krisandro: Been thinking too much of botak babies with small eyes and fat noses lately?
Rei: 210 m/min = (210 × 60) m/hr = 12.6 km/hr ≠ 0.12km/hr
Any slower and you'll have to come and help Miss Loi push the car!
曜
日
ok..i give a better try next time..lol
曜
日
1.
m/min
('.' when t = 0, v = 210 .'.constant of integration = 210)
Speed at 2nd minute =
Miss Loi: Yes the purpose of this first part is to let students be aware of the difference between speed (no minus sign possible) and velocity (minus sign possible).
So performing the standard integration on the acceleration to get your velocity expression, we have:
And sub in v=210 when t=0 (when Miss Loi passed O) we get c = 210, so
Since the question asked for speed, and if the student doesn't have the habit of 'modding' || the expression what like Li-sa did, you'll get v = −150 m/min (after sub t=2) which is the velocity. This means that Miss Loi was actually travelling backwards at the second minute
→ so always remember to remove any − sign in your final answer when you're finding speed and distance!
2. Turning back means that the speed becomes 0 m/min.
.'. Solve
t = 1 or 7
.'.Miss Loi has to turn back at t = 1 minute and t = 7 minutes.
Miss Loi: Those taking Physics would've had this ingrained in their minds - but it's vital to known that at each turning point, there will be this defining Zen-like 'Matrix' moment when everything stops, when there is instantaneous rest ... when v = 0.
With this in mind, we can find the times at the turning points by equating the expression for v we've found in (1) to zero and solve for t, as Li-sa has done, and we find that Miss Loi had to turn back twice ('Matrix'-style) at the first and seventh minutes.
3.
('.' at O, s = 0 .'. constant of integration = 0)
When
.'.The car will stop exactly where the tree fell. Miss Loi will not be able to pass it before it fell.
Miss Loi: Yes to know if Miss Loi managed to get pass the falling tree at O at t = 10, one way is to find out where she is at t = 10, and you'll also need to know what direction she's travelling from during this time. That's when a quick sketch like the one in the next comment below would be really helpful.
Either way we'll need to obtain the expression for displacement s as shown by Li-sa above. Hence:
And sub in s=0 when t=0 (when Miss Loi passed O) we get c = 0, so
So after substituting t = 10 into (2), we get s=100 ⇒ Miss Loi is 100m after point O (think there's a little careless mistake in Li-sa's working above). Also by substituting t = 10 into (1) Miss Loi's velocity is 810 m/min ⇒ she's traveling forward after O so she has definitely passed the falling tree by the tenth minute!
*We can also equate (2) to zero and solve for t, we find that Miss Loi actually reached O earlier at t = 0, 2.13, 9.87.
Total distance she would have travelled in 10 minutes
=
=
=
= 100 - (-1080) + 1080
= 2260 m
Miss Loi: It's important here for students to realize that merely substituting t = 10 into (2) will only give you the displacement from O at t=10.
To get the total distance, you MUST add up the distances travelled at each parted of the journey segmented by the turning points obtained in Part 2 i.e. t=1 & 7.
To do this, you can use Li-sa's integration method above (note her +/&minus signs!) or note the displacements at each segment i.e.
At t = 0, s = 0
At t = 1, s = 100
⇒ total distance travelled from 0 to 1st min = 100
t = 7, s = −980
⇒ total distance travelled from 1st to 7th min = 100+980
t = 10, s = 1000
⇒ total distance travelled from 7th to 10th min = 980+100
∴ Total distance travelled = 100+100+980+980+100 = 2260 m
Again this will be much clearer if you've drawn a sketch of the journey (as shown below) 😉
Unless the tree falls the other way...:(
曜
日
And now that the answers to the question above are out, we have the following expressions for acceleration, velocity and displacement:
a = 60t − 240
v = 30t2 − 240t + 210
s = 10t3 − 120t2 + 210t
With this we can present a sketch of Miss Loi's Initial D-style route among the fallen trees ... complete with some F1-style commentary:
*pops champagne*
While it is not required as part of your final working, it is always desirable to do a quick sketch of a motion diagram like the above to help you visualize the whole journey of the object in the question. This is especially useful when you're asked to calculate the total distance traveled (like part 3 of the question above) or average speed in the kinematics question
曜
日
Time between Miss Loi passing point O and tree falling at point O = 10 - 9.87 = 0.13min = 7.8s.
Speed of Miss Loi when she speed past point O = 763m/min = 45.78km/h.
Can't imagine why Miss Loi's car would crawl under the tree when it looks to fall on her in 7.8 seconds' time.
Anyway, now with a fallen tree at s=0 (i.e. point O) and another at s=100, with Miss Loi's car at 0<s<100, *surprise surprise* Miss Loi still chose to speed past s=100 at 810m/min!!!
Unimaginable horrors... drama indeed. 🙂
曜
日
*beeeeepoooooobeeeeepooooo*