Miss Loi is in serious trouble.
Yesterday she and her sharp tongue had the audacity to question the spending prowess of a smirking young triad chief, sooOOoOo hurting and bruising his ego in the process.
So it was no coincidence this afternoon when a van pulled up suddenly in front of Miss Loi, the moment she stepped out of a shopping centre laden with shopping bags. A group of evil-looking men in shades and black suits quickly jumped out, bundled a startled Miss Loi into the van and zoomed off, crucially leaving behind the shopping items that she’d just gotten at a discount, to her dismay.
Hours later, she found herself gagged and tied up in an old disused oil rig in the middle of the South China Sea! Awaiting, as told by one of the evil-looking men in shades and black suit, her fate at the hands of the smirking young triad chief!
But in true Hong Kong drama fashion, she managed to somehow messaged her hero (played by Louis Koo (古天樂)) via her mobilephone (with her hands tied) before it was taken away. And now her hero is on the way to save her!
Unfortunately when Louis Koo reached his speedboat at the harbour, he realized that he’d forgotten to bring along his trigonometry textbook (香港版)!
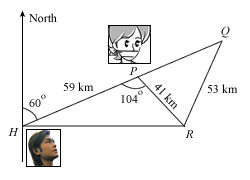
The diagram represents a map showing a harbour H and three oil rigs, P, Q and R, where R is due East of H. HPQ is a straight line which lies on a bearing of 060o and angle HPR = 104o. It is given that HP = 59km, PR = 41km and RQ = 53km.
- The luxury yacht of the smirking young triad chief leaves Q at 0945. It sails directly to R, where it stays for 50 minutes for the chief to indulge in some unspeakable pleasures with some other unfortunate lady held there, before going to P, where Miss Loi is held. When moving, it may be assumed that it travels at a constant speed of 12km/h. At what time does it arrive at P?
- The speedboat, powered by Miss Loi’s hero, has to travel from H to R, as the direct route from H to P is too heavily guarded.
- Calculate the distance between H and R.
- He reckons that he should turn towards P when distance between the speedboat and the oil rig P is the shortest. Calculate this distance and state the point on HR where he should turn.
- Calculate the bearing of R from Q.
- An enemy helicopter, C, is hovering at a point vertically above P. The angle of depression of R from the helicopter is 35o. If there’s a dense layer of cloud at a height of 20km, can the helicopter see the speedboat approaching?
As Miss Loi is not really confident in Louis Koo’s mathematical ability, can someone please pass the following notes to him before he sets off, so that he can reach Miss Loi in time before she gets subjected to any ‘unspeakable pleasures’?
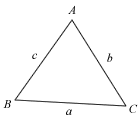
Sine Rule
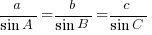
Cosine Rule
a2 = b2+c2-2bc cosA
b2 = a2+c2-2ac cosB
c2 = a2+b2-2ab cosC
Area of triangle
=
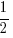bc sinA
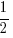=ab sinC
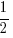=ac sinB
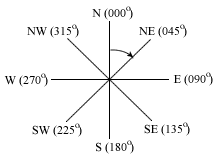
Bearings
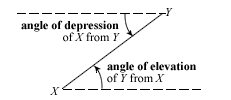
Angles of Elevation & Depression
NOTE: While the question may be similar, do not expect to see cute faces of Miss Loi and Louis Koo appearing in the diagram of your actual E-Maths paper. They are exclusive to 香港版 only.
28 Comments
曜
日
It wasn't me!!!!!
:p
曜
日
*Can't reply you - mouth is gagged*
曜
日
無間道?
Wow, this must be one of the most dramatic post of yours...(u are alway blending, mixing, stiring stuff together with maths)
Hope he or someone save you before Anthony Wang there turn u into his next Cha Shao Bao...
lol at the 香港版
曜
日
*nods head* *gagged*
曜
日
my answers:
1. 1825
2i. 79.6km
2ii. He will turn at 51.1km from H
3. 191.4
4. No, the helicopter is at a height of 28km,
is my answers correct?
曜
日
er for me
1) 8.35 pm
2i)79,56
2ii) 51.1 is where he would turn
3) 191.37
4)YES albeit the heilicopter is 28km above the ground and clearly covered by the clouds. The guys on de speed boat are wearing glasses from the future thus able to see throught de clouds
5) i think miss loi doesnt mind being kidnapped -__- hahas
Since when there's part 5 to this question???
曜
日
1) 1825 hrs
2i)79.5765km
ii) shortest distance = 29.4955km
51.1km from H
3) 191.4
4) No, the helicopter cannot see the speedboat approaching because it is 28.7km from the ground and thus, blocked by the layer of cloud.
曜
日
Haar!!! She can't answer cos I gots her right where I wants her~!
*evil laughter fading into the background*
曜
日
Many thanks to the heroes that have come! Now for the answers ...
For part 1, the total distance the yacht has to travel from Q to R to P = 53km+41km = 94km
So the total travel time
= Distance/Speed
= 94/12 = 7.8333 hrs = 7h50min
But you'll still have to add another 50min of 'unspeakable pleasure' time spent at R, so total time
= 7h50min + 50min
= 8h40min
So if yacht starts at 0945, time of arrival at P
= 0945 + 8h40min
= 1825 (6.25pm)
Kiroii, by wrongly estimating the arrival time of the yacht by more than 2 hours, by the time you reach there, Miss Loi would've been .... oh dun wanna talk about this!
曜
日
For part 2,
Part i
Using the cosine rule you'll get
HR2 = 592 + 412 - 2(59)(41)cos104o
= 79.57km (no problems here for everyone)
Part ii
This part tests you on your knowledge of the area of triangle using different formulae.
First you'll need to understand that the shortest distance from HR to P is the perpendicular distance from HR to P. Let's call this h.
The area of triangle HPR can be found by (1/2)(HP)(PR)sin104o using the formula.
So area of HPR
= (1/2)(59)(41)sin104o
= 1173.57 km2
But pre-pubescent Sec 1 maths also says that area of HPR
= (1/2) x base x height
= (1/2)(HR)h
=(1/2)(79.6)h
So equating both we get
1173.57 km2 = (1/2)(79.6)h
⇒ h = 29.5km (only Noel did this part!)
Lastly to get the point along HR you can simply use Pythagoras theorem i.e.
√(592-29.52)
= 51.1km from H
Simple eh? Think even Louis Koo himself could've done this without his 香港版 trigo textbook!
Straightforward enough eh?
曜
日
For part 3,
Students have to be very careful when reading bearing questions. It says the bearing of R from Q ⇒ the angle is is calculated around Q.
Looking at the following diagram with all the necessary angles highlighted in red:
Remember that you bearing starts from North and goes clockwise, which is the thick red arrow in the diagram).
So bearing
= 360o - 120o - θ
To find θ, we use the sine rule for triangle PQR,
sin76o/53 = sinθ/41
⇒ θ = 48.64o
⇒ bearing = 360o - 120o - 48.64o
= 191.4o
(remember bearing must always be written in 3-digit format!)
曜
日
For part 4,
It's worth noting that the angle of depression of R from C is always equal to the angle of elevation of C from R.
So a triangle is formed as shown:
And you can easily find the height of the helicopter, PC, from:
tan 35o = PC/41
⇒ PC = 28.7km
So since we're at the present where existing technology don't produce glasses that can see through clouds, we can safely assume that Louis Koo will NOT be detected by the helicopter! Moreover, 28.7km is rather high in the sky - almost into the stratosphere - think the crew would've all been frozen!
P.S. Strange though only Noel got exactly the same answer. Why did the rest of you round downwards to 28km???
曜
日
So in the end, as the smirking young triad chief and his 人肉叉焼包…-making henchmen were expecting Louis Koo's impending arrival, an unknown spy codenamed 'Noel' appeared from nowhere, knocked out a few of the henchmen, and rescued Miss Loi from right under their noses!
All this while Louis Koo was still frantically flipping through the pages of his trigo textbook (香港版) at the harbour!
*Sticks out tongue and waves at triad chief now jumping up and down in anger*
曜
日
hmmm...lucky all this happen on escape happens on water...imagine if occur on land, the most of the henchmen in the pic will be in R32, AE85, Rx7 and AE86 drifting behind spy codenamed 'Noel'.
Wah~ seems like i the only one giving nonsense comments here...
曜
日
Hey, Miss Loi was kidnapped by the Triad, not Takumi and Project D!
曜
日
LOL! Liddat also can arh?!
曜
日
HighwayBlogger, are you one of his henchmen in a R32/AE85/Rx7/AE86 drifting on the highway???
C'mon Noel! You need to drive faster and shake him off!
曜
日
Yeah I was in a BM...... bmx lah!
曜
日
wah...u better than me, i in a trishaw...
曜
日
ByPasser, are you the trishaw rider or the passenger? If you're the former, better keep a lookout for three evil Englishmen.
曜
日
haha...be nice Ms Teacher...
曜
日
Teacher. Anything on pi? I am very interested in the magical pi.
曜
日
Maybe next time you may try something like deciphering codes to pass time or to keep up with blogging.
曜
日
Deciphering codes.... Tats my job and tats what i like to do. Now I want to study and know more of the magical pi and its properties.
曜
日
The Math Girl series on YouTube may be helpful if you want to know more about it.
曜
日
Oops, it should be "learn more about it". Sorry for the typo.
曜
日
Thanks. Watching it now.
曜
日
π?
There are two pi posts here!